本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
(本小题满分12分)已知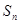 是等差数列
是等差数列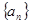 的前
的前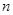 项和,满足
项和,满足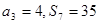 ;
;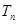 是数列
是数列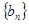 的前
的前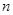 项和,满足:
项和,满足: 。
。
(1)求数列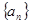 ,
,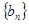 的通项公式;
的通项公式;
(2)求数列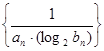 的前
的前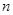 项和
项和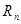
(本小题满分13分)数列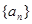 满足
满足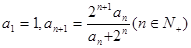
(1)证明:数列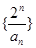 是等差数列;
是等差数列;
(2)求数列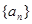 的通项公式
的通项公式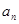 ;
;
(3)设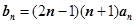 ,求数列
,求数列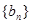 的前
的前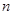 项和
项和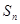 .
.
(本小题满分14分)在△ABC中,角A、B、C所对的边分别是a、b、c满足: 且a,b,c成等比数列,
且a,b,c成等比数列,
(1)求角B的大小;
(2)若 ,求三角形ABC的面积。
,求三角形ABC的面积。
(本小题满分12分)在△ABC中,内角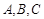 所对的边分别为
所对的边分别为 ,已知
,已知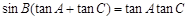 .
.
(1)求证: 成等比数列;
成等比数列;
(2)若 ,求△
,求△ 的面积S.
的面积S.
(本小题满分12分)已知集合 ,
,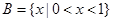 ,U=R.
,U=R.
(1)若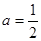 ,求
,求 ;
;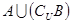 .(2)若
.(2)若 ,求实数a的取值范围。w
,求实数a的取值范围。w