已知函数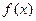 是定义
是定义 在R上的奇函数, 而且单调递增,若实数
在R上的奇函数, 而且单调递增,若实数 ,
, 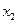 ,
,  满足
满足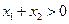 ,
,  ,
,  , 给出下面四个结论:
, 给出下面四个结论:
①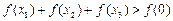 ;②
;② ;
;
③ ; ④
; ④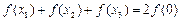
其中一定正确的是 
 (只填序号)
(只填序号)
函数 是定义在
是定义在 上的偶函数,且满足
上的偶函数,且满足 .当
.当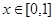 时,
时,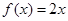 .若在区间
.若在区间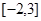 上方程
上方程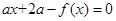 恰有四个不相等的实数根,则实数
恰有四个不相等的实数根,则实数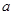 的取值范围为.
的取值范围为.
已知等差数列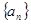 中,有
中,有 成立.类似地,在等比数列
成立.类似地,在等比数列 中,有_____________________成立.
中,有_____________________成立.
在矩形 中,
中,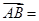
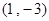 ,
,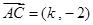 ,则实数
,则实数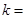 .
.
若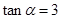 ,则
,则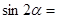 .
.
如果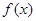 的定义域为
的定义域为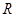 ,对于定义域内的任意
,对于定义域内的任意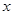 ,存在实数
,存在实数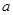 使得
使得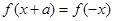 成立,则称此函数具有“
成立,则称此函数具有“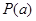 性质”.给出下列命题:
性质”.给出下列命题:
①函数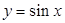 具有“
具有“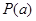 性质”;
性质”;
②若奇函数 具有“
具有“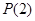 性质”,且
性质”,且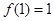 ,则
,则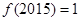 ;
;
③若函数 具有“
具有“ 性质”, 图象关于点
性质”, 图象关于点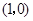 成中心对称,且在
成中心对称,且在 上单调递减,则
上单调递减,则 在
在 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;
④若不恒为零的函数 同时具有“
同时具有“ 性质”和 “
性质”和 “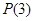 性质”,且函数
性质”,且函数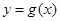 对
对 ,都有
,都有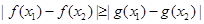 成立,则函数
成立,则函数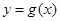 是周期函数.
是周期函数.
其中正确的是(写出所有正确命题的编号).