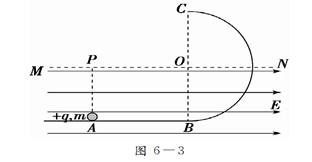
如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接．在过圆心O的水平界面MN的下方分布有水平向右的匀强电场．现有一质量为m、电荷量为＋q的小球从水平轨道上A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场(P点恰好在A点的正上方，如图．小球可视为质点，小球运动到C点之前电荷量保持不变，经过C点后电荷量立即变为零)．已知AB间距离为2R，重力加速度为g.在上述运动过程中，求：电场强度E的大小；
小球在圆轨道上运动时的最大速率；
小球对圆轨道的最大压力的大小．
质量m1=10g的小球在光滑的水平桌面上以v1=30cm/s的速率向右运动，恰好遇上在同一条直线上向左运动的另一个小球．第二个小球的质量为m2=50g，速率v2=10cm/s．碰撞后，小球m2恰好停止．那么，碰撞后小球m1的速度是多大，方向如何？
如图所示，在倾斜角α=37°的斜面上，有一质量为5kg的物体沿斜面滑下，物体与斜面的动摩擦因素μ=0.2，求物体下滑2s的时间内，物体所受各力的冲量。(g=10m/s2，sin37=0.6，cos37=0.8)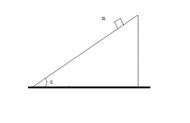
如图所示，质量为m的小球自由下落d后，沿竖直面内的固定轨道ABC运动，AB是半径为d的
光滑圆弧，BC是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点。求：
(1)小球运动到B处时对轨道的压力大小；
(2)小球在BC上运动过程中，摩擦力对小球做的功。(重力加速度为g)
如图所示,物体沿一曲面从A点无初速度滑下,滑至曲面最低点B时,下滑的高度为5m.若物体的质量为1㎏,到B点的速度为6m/s,则在下滑过程中客服阻力所做的功是多少?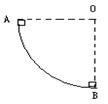
如图所示，一名滑雪运动员经过一段加速滑行后从O点水平飞出，经过3.0s落到斜坡上的A点。已知O点是斜坡的起点，斜坡与水平面的夹角θ=370，运动员的质量m=60kg。不计空气阻力。（取sin370=0.6,cos370=0.8,g取10m/s2）求：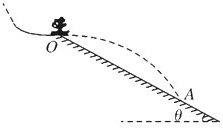
⑴O点与A点的距离L；
⑵运动离开O点时的速度大小；
⑶运动员落到A点时的动能。