已知抛物线C: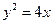
，
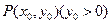为抛物线上一点
，
为
关于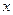
轴对称的点，
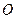为坐标原点.
（1）若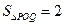
,求点的坐标；
（2）若过满足
（1）中的点作直线
交抛物线
于
两点, 且斜率分别为
，且
，求证：直线
过定点，并求出该定点坐标
如图，四边形ABCD为梯形，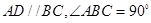
，求图中阴影部分绕A
B旋转一周形成的几何体的表面积和体积.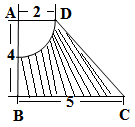
已知
的顶点A（0，1），AB边上的中线CD所在直线方程为
，AC边上的高BH所在直线方程为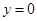
.
（1）求的项点B、C的坐标;
（2）若圆M经过不同的三点A、B、P（m、0），且斜率为1的直线与圆M相切于点P
求：圆M的方程.
如图，长方体
中，
，点E是AB的中点.
（1）证明：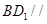
平面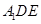
;
（2）证明：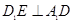
;
（3）求二面角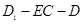
的正切值.
已知圆C的半径为2，圆心在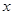
轴正半轴上，直线
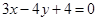与圆C相切
（1）求圆C的方程;
（2）过点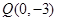
的直线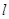
与圆C交于不同的两点
且为
时，求：
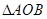的面积.
已知点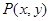
是圆
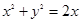上的点
（1）求
的取值范围;
（2）若
恒成立，求实数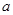
的取值范围.