如框图,当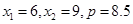 时,
时, 等于()
等于()
| A.7 | B.8 | C.10 | D.11 |
某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是()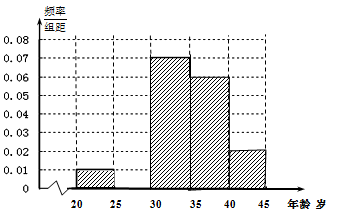
| A.31.6岁 | B.32.6岁 | C.33.6岁 | D.36.6岁 |
五进制数 转化为八进制数是()
转化为八进制数是()
A. |
B. |
C. |
D. |
在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两个样本的下列数字特征相同的是()
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
甲乙两个数学兴趣小组各有5名同学,在一次数学测试中,成绩统计用茎叶图表示,如图所示,若甲、乙小组的平均成绩分别是 ,则下列结论正确的是()
,则下列结论正确的是()
A. ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
B. ,乙比甲成绩稳定 ,乙比甲成绩稳定 |
C. ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
D. ,乙比甲成绩稳定 ,乙比甲成绩稳定 |