(10分)恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地．上市时，外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中．据预测，香菇的市场价格每天每千克将上涨0.5元，但冷库存放这批香菇时每天需要支出各种费用合计340元，而且香菇在冷库中最多保存110天，同时，平均每天有6千克的香菇损坏不能出售．
（1）若存放
天后，将这批香菇一次性出售，设这批香菇的销售总金额为
元，试写出与之间的函数关系式．
（2）李经理想获得利润22500元，需将这批香菇存放多少天后出售？（利润＝销售总金额－收购成本－各种费用）
（3）李经理将这批香菇存放多少天后出售可获得最大利润？最大利润是多少？
环境对人体的影响很大，环保与健康息息相关.目前，家具市场对板材进行了环保认定，其中甲醛含量为一个重要的数据.国家规定每100g板材含甲醛低于40mg的为合格品，含甲醛低于10mg的则为A级产品.某人订做了akgA级板材家具，请你帮助他确定家具中所含的甲醛ymg的范围．
（1）在通过桥洞时会看到如图（1）的标志，这是限制车高的．你知道通过该桥洞车高xm的范围吗？
（2）在通过桥面时会看到如图（2）的标志，这是限制车重的．你知道通过该桥面车重yt的范围吗？
为了了解市场上甲、乙两种手表日走时误差的情况，从这两种手表中各随机抽取10块进行测试，两种手表日走时误差的数据如下（单位：秒）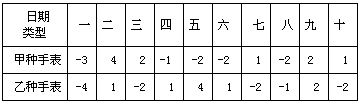
（1）计算甲、乙两种手表日走时误差的平均数；
（2）你认为甲、乙两种手表中哪种手表走时稳定性好？说说你的理由．
某餐厅共有10名工作人员，月工资如下：
解答下列问题：
（1）餐厅所有职工的平均月工资是元？
（2）所有职工工资的中位数是元，众数是元？
（3）该餐厅招聘员工的招聘启示写道：“本餐厅平均月工资1700元以上”，如果你去应聘一般员工，你怎样看待这个招聘启示呢？请用你学过的知识来发表自己的看法吧！
甲、乙两台包装机同时分装质量为400克的奶粉. 从它们各自分装的奶粉中随机抽取了10袋，测得它们的实际质量（单位：克）如下：
甲：401，400，408，406，410，409，400，393，394，394
乙：403，404，396，399，402，401，405，397，402，399
哪台包装机包装的奶粉质量比较稳定？