给出下列命题：①反比例函数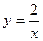
的图象经过一、三象限，且
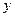随
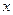的增大而减小；②对角线相等且有一个内角是直角的四边形是矩形；③我国古代三国时期的数学家赵爽，创制了一幅“勾股圆方图”，用形数结合得到方法，给出了勾股定理的详细证明（右图）；④相等的弧所对的圆周角相等.其中正确的是（ ▲ ）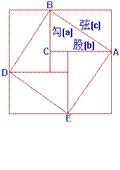
| A．③④ | B．①②③ | C．②④ | D．①②③④ |
如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是（）
A.6 B.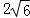
C.
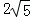D.
点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于（）
A.3 B.2 C.3或5 D.2或6
如图，C、D是线段AB上的两点，且D是线段AC的中点，若AB=10cm，BC=4cm，则AD的长为（）
A.2cm B.3cm C.4cm D.6cm
把一条弯曲的公路改成直道，可以缩短路程．用几何知识解释其道理正确的是（）
| A．两点确定一条直线 | B．垂线段最短 |
| C．两点之间线段最短 | D．三角形两边之和大于第三边 |
如图，AB=12，C为AB的中点，点D在线段AC上，且AD：CB=1：3，则DB的长度为（）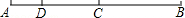
| A．4 | B．6 | C．8 | D．10 |