在平面直角坐标系中,抛物线经过O(0,0)、
A(4,0)、B(3,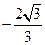 )三点.
)三点.
(1)求此抛物线的解析式;
(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l ,且l与x轴的夹角为30°,若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号)
如图,点 是等边三角形 外接圆的 上一点(与点 , 不重合), 交 于点 .
(1)求证: 是等边三角形;
(2)求证: ;
(3)如果 , ,求 的边长.

某商店计划购进甲、乙两种笔记本,已知2本甲笔记本与3本乙笔记本的总进价为42元,2本甲笔记本与1本乙笔记本的总进价为22元.
(1)求甲、乙两种笔记本的进价分别是多少元?
(2)该商店计划购进两种笔记本共40本,其中甲笔记本的数量不超过乙笔记本的数量,且总金额不超过330元,求共有几种进货方案,并指出哪种方案最省钱.
如图,在正方形 中, 为 的中点,延长 至 ,使 ,过 作 ,垂足为 ,过 作 的垂线交 的延长线于点 .
(1)求证: ;
(2)求证:四边形 是正方形.

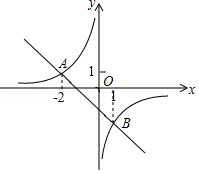
如图,一次函数 的图象与反比例函数 的图象交于点 , .
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式 的解集.
某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分)
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表:
|
年级 |
最高分 |
平均分 |
众数 |
方差 |
|
七年级 |
98 |
94 |
|
7.6 |
|
八年级 |
98 |
94 |
93 |
|
根据以上信息,完成下列问题:
(1)填空: ;
(2)求表中 的值,并判断两个年级中哪个年级成绩更稳定;
(3)七年级两名最高分选手分别记为: , ,八年级第一、第二名选手分别记为: , ,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.