如图,四棱锥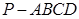 中,底面是以
中,底面是以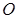 为中心的菱形,
为中心的菱形,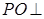 底面
底面 ,
,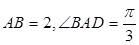 ,
,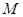 为
为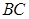 上一点,且
上一点,且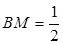 .
.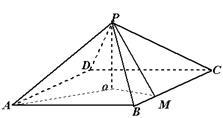
(1)证明: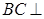 平面
平面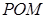 ;
;
(2)若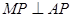 ,求四棱锥
,求四棱锥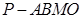 的体积.
的体积.
已知函数f(x)=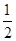 sin2x-
sin2x-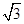
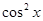 .
.
(Ⅰ)求f(x)的最小周期和最小值,
(Ⅱ)将函数f(x)的图像上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图像.当x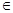
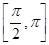 时,求g(x)的值域.
时,求g(x)的值域.
甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直每人都已投球3次时投篮结束,设甲每次投篮投中的概率为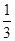 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为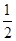 ,且各次投篮互不影响.
,且各次投篮互不影响.
(Ⅰ)求乙获胜的概率;
(Ⅱ)求投篮结束时乙只投了2个球的概率.
已知 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 的前
的前 项和.
项和.
(1)求 及
及 ;
;
(2)设 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 的通项公式及其前
的通项公式及其前 项和
项和 .
.
设函数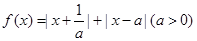 .
.
(1)证明: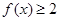 ;
;
(2)若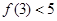 ,求
,求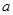 的取值范围.
的取值范围.