做初速度为零的匀加速直线运动的物体在时间T 内通过位移s1到达A点,接着在时间T内又通过位移s2到达B点,则以下判断正确的是( )
A.物体在A点的速度大小为 |
B.物体运动的加速度为 |
C.物体运动的加速度为 |
D.物体在B点的速度大小为 |
在图中a、b所示的两电路中,电阻R、电流表、电压表都是相同的,电池的内阻相对于电阻R的大小可以忽略。闭合开关后,图a和b电路中电压表和电流表的示数, 和
和 的大小不相同,它们的关系是
的大小不相同,它们的关系是
① ②
②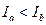
 ③
③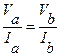 ④
④

其中正确的是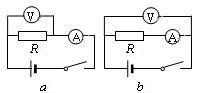
| A.①③ | B.①④ | C.②③ | D.②④ |
以下关于电流表与电压表的说法中,正确的是
| A.都是用电流表G与电阻并联改装而成的 |
| B.都是用电流表G与电阻串联改装而成的 |
| C.它们本身都有内阻,只是电流表的内阻一般很小,而电压表的内阻一般很大 |
| D.电流表的内阻肯定比用来改装的电流表G的内阻大,而电压表的内阻肯定比用来改装的电流表G的内阻小 |
现有经过精确校准的电压表V1和V2,当分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数依次为12.7V和12.3V,则:
①a、b间的实际电压略大于12.7V ②a、b间的实际电压略小于12.3V
③电压表V1的内阻大于V2的内阻 ④电压表V1的内阻小于V2的内阻
以上判断正确的是
| A.①③ | B.②④ | C.①④ | D.②③ |
如图所示的电路,R1=10Ω,R2=8Ω,电池有内阻,K接1时,伏特表示数为2V,则K接2时伏特表示数可能为
| A.2.2V | B.2.9V | C.1.7V | D.1.4V |

如图所示是一个由电池、电阻R与平行板电容器组成的串联电路,在增大电容器两极板间距离的过程中
| A.电阻R中没有电流 | B.电容器的电容变大 |
| C.电阻R中有从a流向b的电流 | D.电阻R中有从b流向a的电流 |