如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=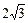
，直线y=
经过点C，交y轴于点G,且∠AGO=30°。
（1）点C、D的坐标分别是C（ ），D（ ）；
（2）求顶点在直线y=上且经过点C、D的抛物线的解析式；
（3）将（2）中的抛物线沿直线y=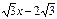
平移，平移后的抛物线交y轴于点F，顶点为点E。平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存
在，请求出此时抛物线的解析式；若不存在，请说明理由。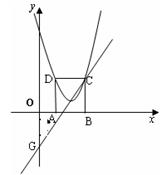
某电视台与某广告公司约定播放甲、乙两部电视剧，经调查，播放甲连续剧平均每集有观众20万人次，播放乙连续剧平均每集有观众15万人次，公司要求电视台每周共播放7集。
（1）设一周内甲连续剧播x集，甲、乙两部连续剧的观众总收视人数为y万人次，求y与x的函数关系式；
（2）已知电视台每周只能为该公司提供不超过300分钟的播放时间，并且播放甲连续剧每集50分钟，播放乙连续剧每集35分钟，问电视台每周应各播放甲、乙两种连续剧多少集，才能使每周收视观众的人数总和最大？并求出这个最大值。
已知一次函数y=x+2
（1）在平面直角坐标系内画出函数y=x+2的图像 ；
（2）求当x=2时，y的值；
已知，如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D.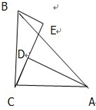
求证：△BEC≌△CDA．
先化简，再求值：[（x-y）2+（x+y）（x-y）]÷2x，其中x=3，y=—1.5 .
将下列各式分解因式：（1）x3－x；（2）－x2y＋2xy2－y3．