某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套。
(1)若设第二个月的销售定价每套增加x元,填写下表。
| 时间 |
第一个月 |
第二个月 |
| 每套销售定价(元) |
|
|
| 销售量(套) |
|
|
(2)若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套多少元?
如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.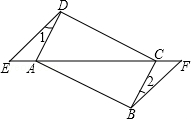
如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(﹣4,2)、B(﹣2,3)、C(﹣1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.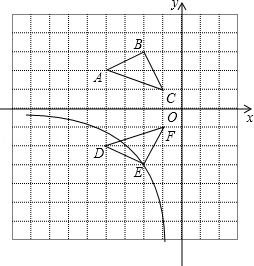
当a=2014时,求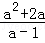 ÷(a+
÷(a+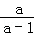 )的值.
)的值.
锐角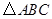 中,
中,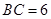 ,
,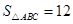 ,两动点
,两动点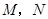 分别在边
分别在边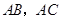 上滑动,且
上滑动,且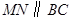 ,以
,以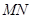 为边向下作正方形
为边向下作正方形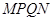 ,设其边长为
,设其边长为 ,正方形
,正方形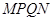 与
与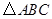 公共部分的面积为
公共部分的面积为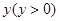 .
.
(1)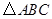 中边
中边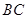 上高
上高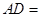 ;
;
(2)当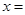 时,
时,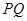 恰好落在边
恰好落在边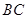 上(如图1);
上(如图1);
(3)当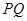 在
在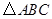 外部时(如图2),求
外部时(如图2),求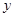 关于
关于 的函数关系式(注明
的函数关系式(注明 的取值范围),并求出
的取值范围),并求出 为何值时
为何值时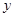 最大,最大值是多少?
最大,最大值是多少? 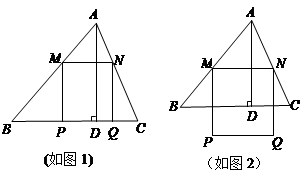
如图,已知Rt△ABC中,∠C=90°,CB=8,CA=6.
(1)求作⊙O,使⊙O过点C,圆心O在CB上,且与边AB相切(用尺规作图,不写作法,保留痕迹)
(2)求⊙O的半径