已知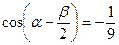 ,
,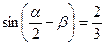 ;且
;且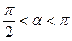 ,
,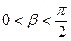
求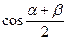
(本小题满分12分)某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率依次为 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,函数
时,函数 恰有3个零点,求实数
恰有3个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,有
,有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知一个袋子中有3个白球和3个红球,这些球除颜色外完全相同.
(Ⅰ)每次从袋中取出一个球,取出后不放回,直到取到一个红球为止,求取球次数 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)每次从袋中取出一个球,取出后放回接着再取一个球,这样取3次,求取出红球次数 的数学期望
的数学期望 .
.
(本小题满分10分)已知函数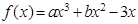 在
在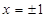 处取得极值.
处取得极值.
(Ⅰ)求实数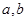 的值;
的值;
(Ⅱ)过点 作曲线
作曲线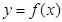 的切线,求此切线方程.
的切线,求此切线方程.
(本小题满分10分)
(Ⅰ)证明: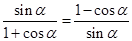 .
.
(Ⅱ)已知圆的方程是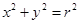 ,则经过圆上一点
,则经过圆上一点 的切线方程为
的切线方程为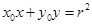 ,类比上述性质,试写出椭圆
,类比上述性质,试写出椭圆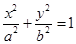 类似的性质.
类似的性质.