在平面直角坐标系xOy中,反比例函数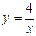 的图象与抛物线
的图象与抛物线
交于点A(3, n).
(1)求n的值及抛物线的解析式;
(2) 过点A作直线BC,交x轴于点B,交反比例函数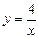 (
( )的图象于点C,且AC=2AB,求B、C两点的坐标;
)的图象于点C,且AC=2AB,求B、C两点的坐标;
(3)在(2)的条件下,若点P是抛物线对称轴上的一点,且点P到x轴和直线BC的距离相等,求点P的坐标.
计算: 
计算: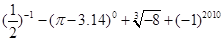
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2。
已知点A是数轴上的点,完成下列各题:
如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
如果点A表示的数是-4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________。
某中学初一(四)班3位教师决定带领本班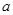 名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。
名学生在五一期间去北京旅游,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律八折优惠。已知这两家旅行社的基本价一样,都是每人500元。
(1)分别用整式表示参加这两家旅行社所需的费用。
(2)如果这3位教师要带领该班30名学生参加旅游,你认为选择哪一家旅行社较为合算,为什么?
某出租车从停车场出发,沿着东西向的大街行驶,到晚上6时,一天的行驶记录如下:(向东行驶记为正,向西行驶记为负,单位:千米)-4、+7、-9、+8、+6、-4、-3、+12
(1)到晚上6时,出租车在什么位置?
(2)若汽车每千米耗油0.2升,则从停车场出发到晚上6时,出租车共耗油多少升?