如图,在△ABC中,分别以AB,AC为直径在△ABC外作半圆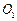 和半圆
和半圆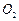 ,其中
,其中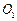 和
和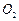 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 
(1)连结 ,
,
证明: ;
;
(2)如图,过点A分别作半圆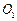 和半圆
和半圆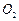 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;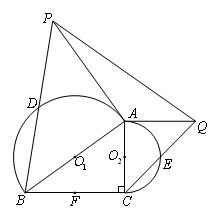
(3)如图三,过点A作半圆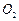 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线.
的切线.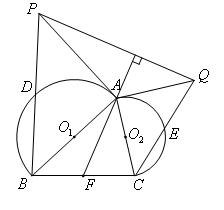
如图,△ABC中,D为AC边上一点,DE⊥BC于点E,若AD=2DC,AB=4DE,求sinB的值。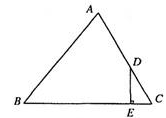
先化简再求值:(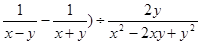 ,其中x=1+
,其中x=1+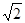 ,y=1-
,y=1-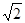 ;
;
.已知关于x的方程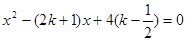
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长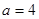 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。
. 阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2 =(1+
=(1+ )
)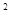 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b =(m+n
=(m+n )
)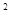 (其中a、b、m、n均为正整数),则有a+b
(其中a、b、m、n均为正整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,
,
∴a= m2+2n2,b=2mn.这样小明就找到了一种把部分a+b 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b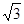 =(m+n
=(m+n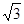 )
)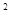 ,用含m、n的式子分别表示a、b,得:a=,b= ;
,用含m、n的式子分别表示a、b,得:a=,b= ;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:+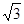
=(+ 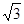 )
)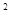 ;
;
(3)若a+4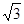 =(m+n
=(m+n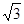 )
)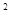 ,且a、m、n均为正整数,求a的值.
,且a、m、n均为正整数,求a的值.
先化简再计算: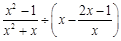 ,其中x是一元二次方程
,其中x是一元二次方程 的正数根.
的正数根.