已知双曲线

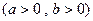 与圆
与圆 相切,过
相切,过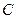 的一个焦点且斜率为
的一个焦点且斜率为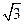 的直线也与圆
的直线也与圆 相切.
相切.
(Ⅰ)求双曲线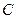 的方程;
的方程;
(Ⅱ)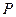 是圆
是圆 上在第一象限的点,过
上在第一象限的点,过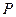 且与圆
且与圆 相切的直线
相切的直线 与
与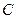 的右支交于
的右支交于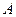 、
、 两点,
两点, 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
已知数列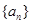 的前
的前 项和为
项和为 ,且
,且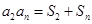 对一切正整数
对一切正整数 都成立.
都成立.
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)设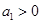 ,数列
,数列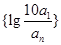 的前
的前 项和为
项和为 ,当
,当 为何值时,
为何值时, 最大?并求出
最大?并求出 的最大值.
的最大值.
已知函数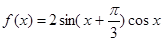 .
.
(Ⅰ)求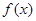 的值域;
的值域;
(Ⅱ)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知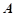 为锐角,
为锐角,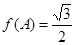 ,
,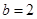 ,
,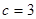 ,求
,求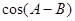 的值.
的值.
设有关于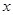 的一元二次方程
的一元二次方程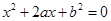 .
.
(Ⅰ)若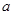 是从
是从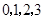 四个数中任取的一个数,
四个数中任取的一个数,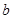 是从
是从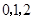 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若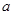 是从区间
是从区间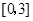 任取的一个数,
任取的一个数,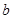 是从区间
是从区间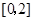 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
已知在△ABC中,内角A,B,C所对的边长分别为a,b,c,且tan A+tan B=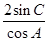 .
.
(1)求角B的大小;
(2)若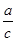 +
+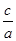 =3,求sin Asin C的值.
=3,求sin Asin C的值.
设函数f(x)=x2+|x-2|-1,x∈R.
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值.