(本小题满分12分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: =
= 若不建隔热层,每年能源消耗费用为8万元.设
若不建隔热层,每年能源消耗费用为8万元.设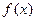 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及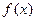 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用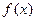 达到最小,并求最小值.
达到最小,并求最小值.
一块形状为直角三角形的铁皮,直角边长分别为40cm与60cm现将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪法,才能使剩下的残料最少?
已知函数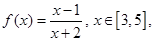 求函数
求函数 的最大值和最小值.
的最大值和最小值.
设A={-1,1,3},B={a+2,a2+4},A∩B={3},求实数a的取值范围 ,
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: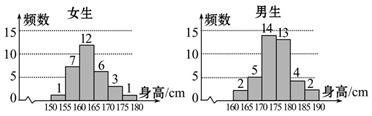
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185 cm之间的概率;
(3)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.
某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表:
已知:
(1)求 ;
;
(2)画出散点图;你从散点图中发现该种服装的销售件数x与纯利润y(元)之间有什么统计规律吗?
(3)求纯利y与每天销售件数x之间的线性回归方程;
(4)若该周内某天销售服装20件,估计可获纯利多少元?