给出下列命题:
(1)存在实数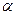 ,使
,使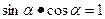 ;
;
(2)函数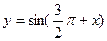 是偶函数;
是偶函数;
(3)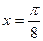 是函数
是函数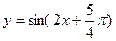 的一条对称轴;
的一条对称轴;
(4)若 是第一象限的角,且
是第一象限的角,且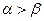 ,则
,则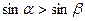 ;
;
(5)将函数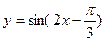 的图像先向左平移
的图像先向左平移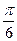 ,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为
,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为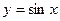 .
.
其中真命题的序号是
已知实数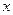 、
、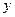 满足
满足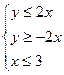 ,则
,则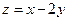 的最小值是
的最小值是
已知等比数列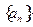 各项均为正数,若
各项均为正数,若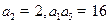 ,则
,则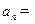
观察下列等式:
① cos2α="2" cos2 α-1;
② cos 4α="8" cos4α-8 cos2α+1;
③ cos 6α="32" cos6 α-48 cos4α+18 cos2α-1;
④ cos 8α=" 128" cos8α-256cos6 α+160 cos4α-32 cos2α+1;
⑤ cos 10α=mcos10α-1280 cos8α+1120cos6 α+ncos4α+p cos2α-1;
可以推测,m-n+p=________。
老师给出一个函数,四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于任意x∈R,都有f(1+x)=f(1-x);
乙:在(-∞,0]上,函数f(x)单调递减;
丙:在(0,+∞)上,函数f(x)单调递增;
丁:f(0)不是函数f(x)的最小值。
如果其中有三个人说得正确,则这个函数f(x)的解析式可能是_______。
曲线 在点(0,1)处的切线方程为 。
在点(0,1)处的切线方程为 。