如图，在平面直角坐标系中，直线l：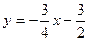
沿x轴翻折后，与x轴交于点A，与y轴交于点B，抛物线
与y轴交于点D，与直线AB交于点E、点F（点F在点E的右侧）．
（1）求直线AB的解析式；
（2）若线段DF∥x轴，求抛物线的解析式；
（3）如图，在（2）的条件下，过F作FH⊥x轴于点G，与直线l交于点H，在抛物线上是否存在P、Q两点（点P在点Q的上方），PQ与AF交于点M，与FH交于点N，使得直线PQ既平分△AFH的周长，又平分△AFH面积，如果存在，求出P、Q的坐标，若不存在，请说明理由．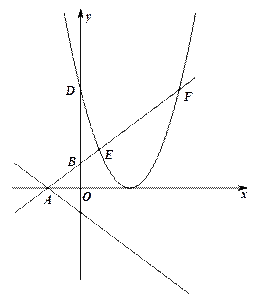
有一种“24点”的游戏，其规则是：任取4个数，将这4个数（每个数只能用一次）进行加、减、乘、除混合运算，使其结果为24。例如：1，2，3，4，做运算：（1+2+3）×4=24。现有2组数据，请运用上述规则写出一条运算式，使其结果等于24。
（1）2、3、4、6 运算式子为： ______=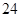
.
（2）
、
、-
、7运算式子为： _______=.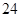
用火柴棒按下面的方式搭图形
（1）把下表填完整：
(2)第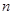
个图形需要___________根小棒；第10个图形需要_______根小棒。
把下列各数在数轴上表示出来，并用“＜”号把这些数连接起来．
－3，
,－(－1.5)，
⑴如图，在△ABC中，∠ABC的平分线BF交AC于F，过点F作DF∥BC，求证：BD=DF。
⑵如图，在△ABC中，∠ABC的平分线BF与∠ACB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E。那么BD，CE，DE之间存在什么关系？并证明这种关系。
⑶如图，在△ABC中，∠ABC的平分线BF与∠ACB的外角平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E。那么BD，CE，DE之间存在什么关系？请写出你的猜想。（不需证明）
某企业两年前创办时的资金是1000万元，现在已有资金1440万元。求该企业这两年内资金的年平均增长率。