(10分)如图,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.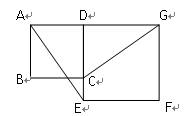
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图,连接AE和GC. 你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.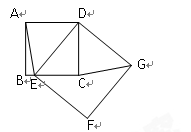
(本小题满分12分)阅读下列内容,设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若 ,则该三角形是直角三角形;②若
,则该三角形是直角三角形;②若 ,则该三角形是钝角三角形;③
,则该三角形是钝角三角形;③ ,则该三角形是锐角三角形.
,则该三角形是锐角三角形.
例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 ,故由上面③可知该三角形是锐角三角形,请解答以下问题:
,故由上面③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是三角形;
(2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形,则x的值为;
(3)若一个三角形的三条边长分别是 ,
, ,
, 请判断这个三角形的形状,并写出的判断过程.
请判断这个三角形的形状,并写出的判断过程.
(本小题满分10分)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)
(本小题满分10分)甲、乙两人分别从相距72千米的A,B两地同时出发,相向而行.甲从A地出发,走了2千米时,发现有物品遗忘在A地,便立即返回,取了物品后立即从A地向B地行进,结果甲、乙两人恰好在AB的中点处相遇.若甲每时比乙多走1千米,求甲、乙两人的速度.
解下列方程和方程组(每小题4分,共8分)
(1)
(2)
(本小题满分8分)
①化简
②化简并求值 然后从2,-2,3中任选一个你喜欢的a的值代入求值.
然后从2,-2,3中任选一个你喜欢的a的值代入求值.