已知二次函数 的图象过点(1,13),且函数
的图象过点(1,13),且函数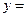
 是偶函数.
是偶函数.
(1)求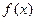 的解析式;
的解析式;
(2)已知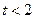 ,
,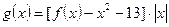 ,求函数
,求函数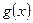 在[
在[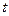 ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(3)函数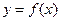 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
设Sn是等差数列{an}的前n项和,已知 S3,
S3, S4的等比中项为
S4的等比中项为 S5;
S5;  S3,
S3, S4的等差中项为1,求数列{an}的通项公式.
S4的等差中项为1,求数列{an}的通项公式.
等差数列{an}的奇数项的和为216,偶数项的和为192,首项为1,项数为奇数,求此数列的末项和通项公式.
已知数列{an}中,a1= ,an=2-
,an=2- (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).
(1)求证:数列{bn}是等差数列;
(2)求数列{an}中的最大项和最小项,并说明理由.
等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?
设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列 的前n项和,求Tn.
的前n项和,求Tn.