对于函数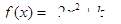 ,当实数
,当实数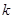 属于下列选项中的哪一个区间时,才能确保一定存在实数对
属于下列选项中的哪一个区间时,才能确保一定存在实数对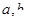 (
( ),使得当函数
),使得当函数 的定义域为
的定义域为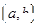 时,其值域也恰好是
时,其值域也恰好是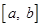
A.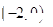 |
B.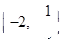 |
C.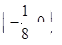 |
D.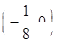 |
实数 是图象连续不断的函数
是图象连续不断的函数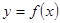 定义域中的三个数,且满足
定义域中的三个数,且满足 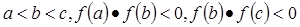 ,则函数
,则函数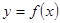 在区间
在区间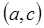 上的零点个数为( )
上的零点个数为( )
| A.2 | B.奇数 | C.偶数 | D.至少是2 |
世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口就可相当于一个()
| A.新加坡(270万) | B.香港(560万) |
| C.瑞士(700万) | D.上海(1200万) |
已知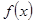 是偶函数,它在
是偶函数,它在 上是减函数,若
上是减函数,若 ,则
,则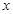 的取值范 围是()
的取值范 围是()
A.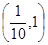 |
B.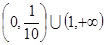 |
C.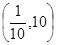 |
D. |
已知函数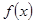 是
是 上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么
上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么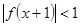 的解集的补集是()
的解集的补集是()
| A.(-1,2) | B.(1,4) |
C. |
D.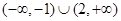 |
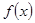 是定义在[-6,6]上的偶函数,且
是定义在[-6,6]上的偶函数,且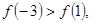 则下列各式一定成立的是()
则下列各式一定成立的是()
A.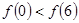 |
B.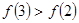 |
C.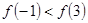 |
D. |