在直角坐标系中,横、纵坐标都为整数的点叫做整点,设坐标轴的单位长为1cm,整点P从原点O出发,速度为1cm/秒,且点P只能向上或向右运动.请回答下列问题:
(1)填表:
| P从O出发的时间 |
可以得到的整点的坐标 |
可以得到的整点的个数 |
| 1秒 |
(0,1)、(1,0) |
2 |
| 2秒 |
(2,0)、(0,2)、() |
3 |
| 3秒 |
(3,0)、(0,3)、()、() |
4 |
(2)当点P从点O出发10秒时,可得到的整点的个数是_________个;
(3)当点P从O点出发__________秒时,可得到整点(10,5);
(4)当点P从点O出发30秒时,整点P恰好在直线y=2x-6上,请求P点坐标.
如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
设一次函数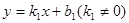 的图象为
的图象为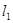 ,一次函数
,一次函数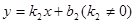 的图象为直线
的图象为直线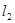 ,若
,若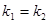 ,且
,且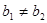 ,我们就称直线
,我们就称直线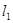 与直线
与直线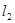 互相平行.解答下面的问题:
互相平行.解答下面的问题: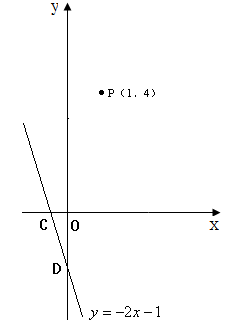
(1)求过点P(1,4)且与已知直线 平行的直线的函数表达式,并画出直
平行的直线的函数表达式,并画出直
线的图象;
(2)设(1)中的直线分别与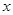 轴、y轴交于A、B两点,直线
轴、y轴交于A、B两点,直线 分别与
分别与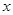 轴、
轴、
y轴交于C、D两点,求四边形ABCD的面积.
某校为绿化校园,计划购买13600元树苗,并且希望这批树苗的成活率为92%.已知:甲种树苗每株50元,乙种树苗每株10元;甲、乙两种树苗的成活率分别为90%和95% .求:甲、乙两种树苗各购多少株?
下表是八年级(1)班10名学生数学测试成绩统计表:
| 成绩 |
50 |
60 |
70 |
80 |
90 |
| 人数(人) |
1 |
2 |
x |
y |
2 |
(1)若这10名学生成绩的平均数为73分,求x和y的值.
(2)设这个班10名学生成绩的众数为a,中位数为b,求a、b的值.