甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的的加速度大小减小为原来的一半。求甲乙两车在这两段时间间隔内走过的总路程之比?
(19分)如图a所示,水平直线MN下方有竖直向上的匀强电场,现将一重力不计、比荷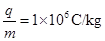 的正电荷置于电场中的O点由静止释放,经过
的正电荷置于电场中的O点由静止释放,经过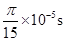 后,电荷以
后,电荷以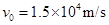 的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).计算结果可用π表示。
的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).计算结果可用π表示。
(1)求O点与直线MN之间的电势差;
(2)求图b中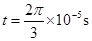 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;
(3)如果在O点右方d=67.5cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间。
如图为某工厂生产流水线上水平传输装置的俯视图,它由传送带和转盘组成。物品(质量m=1kg)从A处无初速放到传送带上,运动到B处后进入匀速转动的转盘,设物品进入转盘时速度大小不发生变化,并随转盘一起运动(无相对滑动),到C处被取走装箱。已知A、B两处的距离L=9m,传送带的传输速度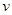 =2.0m/s,物品在转盘上与轴O的距离R=5m,物品与传送带间的动摩擦因数
=2.0m/s,物品在转盘上与轴O的距离R=5m,物品与传送带间的动摩擦因数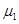 =0.2。取g=10m/s2。
=0.2。取g=10m/s2。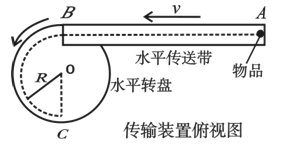
(1)物品从A处运动到B处的时间t;
(2)物品从A处运动到C处的过程中外力对物品总共做了多少功
(3)若物品在转盘上的最大静摩擦力可视为与滑动摩擦力大小相等,则物品与转盘间的动摩擦因数 至少为多大?
至少为多大?
“神舟”六号载人飞船在空中环绕地球做匀速圆周运动,某次经过赤道的正上空时,对应的经度为θ1(实际为西经157.5°),飞船绕地球转一圈后,又经过赤道的正上空,此时对应的经度为θ2(实际为180°).已知地球半径为R,地球表面的重力加速度为g,地球自转的周期为T0.求飞船运行的圆周轨道离地面高度h的表达式.(用θ1、θ2、T0、g和R表示)
如图所示,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.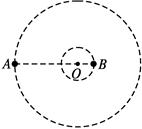
(1)求两星球做圆周运动的周期.
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期为T2.已知地球和月球的质量分别为5.98×1024 kg和7.35×1022 kg.求T2与T1两者平方之比.(结果保留三位小数)
登月舱在离月球表面112 km的高空绕月球运行,运行周期为120.5 min,已知月球半径为1.7×103 km,试估算月球的质量.