如图所示的电路中，两平行金属板A、B水平放置，两板间
的距离d="40" cm。电源电动势E=24V
,内电阻r=1Ω，电阻R=15Ω。闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度V0="4" m/s竖直向上射入板间。若小球带电量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力。 (取g="10" m/s2)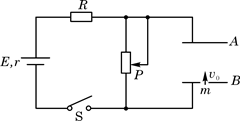
滑动变阻器接入电路的阻值
为多大时，小球恰能到达A板?此时，电源的输出功率是多大?
如图所示,半径为R､内壁光滑的空心圆筒放在地上,将两个重力都是G､半径都是r的球(R<2r<2R)放在圆筒中,求:
(1)筒底对球A的弹力?
(2)筒壁对球A的弹力是否大于筒壁对球B的弹力?
(3)球A对球B的弹力一定大于重力G吗?
(4)球B对筒壁的压力一定小于重力G吗?
(8分)如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：
(1)弹簧对木块所做的功；
(2)木块从B到C过程中克服摩擦力做的功；
(12分)人拉原来静止的重300N的车在水平路面上前进,拉力大小为20N,方向斜向上且与水平方向成300角,车前进500米,车与路面的动摩擦因数为0.03,求:
(1)拉力对车所做的功;
(2)摩擦力对车所做的功;
(3)车获得的动能.
为了实现登月计划，先要测算地月之间的距离。已知地球表面重力加速度为g，地球半径为R，在地面附近物体受到地球的万有引力近似等于物体在地面上的重力，又知月球绕地球运动的周期为T，万有引力常量为G。则：
（1）地球的质量为多少？
（2）地月之间的距离为多少？（用已知量表示）
水平轨道PQ、MN两端各接一个阻值R1=R2=8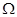
的电阻，轨道间距L=1.0m，轨道很长，轨道电阻不计。轨道间磁场按如图所示的规律分布，其中每段垂直纸面向里和向外的磁场区域宽度均为10cm，磁感应强度大小均为B=1.0T，每段无磁场的区域宽度均为20cm，导体棒ab本身电阻r=1.0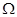，导体棒与导轨接触良好。现使导体棒ab以
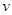=1.0m/s的速度始终向右匀速运动。求：
（1）当导体棒ab从左端进入磁场区域开始计时，设导体棒中电流方向从b流向a为正方向，通过计算后请画出电流随时间变化的i－t图像；
（2）整个过程中流过导体棒ab的电流为交变电流，求出流过导体棒ab的电流有效值。（结果保留2位有效数字）