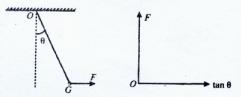
如图所示,一根轻绳上端固定住0点,下端拴一个重为G的钢球,球处于静止状态,现对球施加一个方向始终保持水平的外力F,使球缓慢地移动,在移动过程中的每一时刻,均可认为球处于平衡状态,若要保证轻绳不被拉断,绳与竖直方向夹角θ必须满足θ≤60°,求:轻绳可以承受的拉力F1的最大值;
在F-tan θ坐标系中画出外力F与tanθ的关系图象。
驾驶证考试中的路考,在即将结束时要进行目标停车,考官会在离停车点不远的地方发出指令,要求将车停在指定的标志杆附近,终点附近的道路是平直的,依次有编号为A.B.C.D.E的5根标志杆,相邻杆之间的距离 。一次路考中,学员驾驶汽车。假设在考官发出目标停车的指令前,汽车是匀速运动的,当车头经过O点考官发出指令:“在D标志杆目标停车”,同时计时器开始计时,学员需要经历
。一次路考中,学员驾驶汽车。假设在考官发出目标停车的指令前,汽车是匀速运动的,当车头经过O点考官发出指令:“在D标志杆目标停车”,同时计时器开始计时,学员需要经历 的反应时间才开始刹车,幵始刹车头距O点x0=8m,刹车后汽车做匀减速直线运动。计时器显示从计时开始到车头到达B杆时间为tB=4.5s,已知LOA=44m,求:
的反应时间才开始刹车,幵始刹车头距O点x0=8m,刹车后汽车做匀减速直线运动。计时器显示从计时开始到车头到达B杆时间为tB=4.5s,已知LOA=44m,求:
(1)刹车前汽车做匀速运动的速度大小v0;
(2)汽车开始刹车后做匀减速直线运动的加速度大小a;
(2)计时器显示为9s时,车头离D的距离。
2015年9月3日纪念抗日战争胜利70周年阅兵式上,我国是“歼十”直升机方阵接受世界的检阅,如图所示,一直升机在地面上空高度A位置处于静止状态待命,要求该机在11时16分40秒由静止开始沿水平方向做匀加速直线运动,经过AB段加速后,以40m/s的速度进入BC段的匀速表演区域,11时20分准时通过C位置.已知xAB=4km,xBC=8km.求:重·庆※名-校—资.源~库编辑
(1)在AB段做匀加速直线运动时的加速度大小是多少?
(2)AB段的长度为多少?
如图所示,质量为4kg的物体静止在水平面上,物体与水平面间的动摩擦因数为0.5,t=0时物体受到大小为20N与水平方向成37°角斜向上的拉力F作用,沿水平面做匀加速运动,拉力作用4s后撤去,(g取10m/s2,sin37°=0.6,cos37°=0.8)求: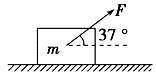
(1)撤去拉力时物体的速度大小
(2)物体从出发到停止的总位移大小
如图,倾角为37°的斜面上一重力为50N的木块恰好匀速下滑,sin37° = 0.6.求:
(1)木块所受到的摩擦力为多少?
(2)木块与斜面间的动摩擦因数为多少?
(3)用平行斜面的力向上推木块匀速上滑,该推力为多大?
学校每周一都会举行升旗仪式,小明是学校的升旗手,已知国歌从响起到结束的时间是48s,旗杆高度是19m,红旗从离地面1.4m处开始升起.小明从国歌响起时开始升旗,若设小明升旗时先拉动绳子使红旗向上匀加速直线运动,时间持续4s,然后使红旗做匀速直线运动,最后使红旗做匀减速直线运动,加速度大小与开始升起时的加速度大小相同,国歌结束时红旗刚好到达旗杆的顶端且速度为零.试求:
(1)计算小明升旗时红旗的位移s和匀速直线运动的时间t.
(2)红旗匀速直线运动的速度大小v.
(3)使红旗向上做匀加速直线运动时加速度的大小a.