如右图所示装置可用来验证机械能守恒定律。摆锤A拴在长L的轻绳一端，另一端固定在O点，在A上放—个小铁片，现将摆锤拉起，使绳偏离竖直方向成θ角时由静止开始释放摆锤，当其到达最低位置时，受到竖直挡板P阻挡而停止运动，之后铁片将飞离摆锤而做平抛运动。
为了验证摆锤在运动中机械能守恒，必须求出摆锤在最低点的速度。为了求出这一速度，实验中还测量了遇到挡板之后铁片的水平位移S和竖直下落高度h。根据测得的物理量表示摆锤在最低点的速度v=
根据巳知的和测得的物理量，写出摆锤在运动中机械能守恒的关系式为 。
若用一张印有小方格的纸记录轨迹，小方格的边长为L，小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的计算式为v0="" （用L
、g表示）。
月球质量是地球质量的
，月球半径约是地球半径的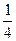
，月球到地球球心的距离是地球半径的60倍，则月球表面重力加速度是地球表面重力加速度的倍，月球轨道处的重力加速度是地球表面重力加速度的 倍，月球的第一宇宙速度是地球的第一宇宙速度的___倍。（用分数表示）
两颗人造卫星A、B的质量之比mA∶mB=1∶2，轨道半径之比rA∶rB=1∶3，某一时刻它们的连线通过地心，则此时它们的线速度之比vA∶vB="" ，向心加速度之比 , 向心力之比FA∶FB="" 。
长度为L="0.50" m的轻质细杆OA，A端有一质量为m="3.0" kg的小球，如图所示，小球以O点为圆心，在竖直平面内做圆周运动，通过最高点时，小球的速率是v="2.0" m/s ，g取10 m/s2，则小球受到作用力为 N，方向向。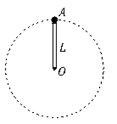
小船匀速横渡一条宽120m的河流，当船头垂直于河岸方向航行时，30s到达河对岸下游60m处，则船在静水中的速度为；若船头保持与河岸上游成α角航行，恰好到达正对岸，则α=。