如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”。如4=22-02,12=42-22,20=62-42,因此,4,12,20这三个数都是神秘数。28和2012这两个数是神秘数吗?为什么?
设两个连续偶数为2k+2和2k(其中k取非负数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
两个连续奇数的平方差(取正数)是神秘吗?为什么?
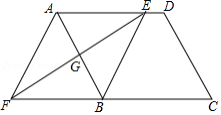
如图,在平行四边形 中,边 的垂直平分线交 于点 ,交 的延长线于点 ,连接 , .
(1)求证: ;
(2)试判断四边形 的形状,并说明理由.
如图,抛物线 经过点 , ,直线 交 轴于点 ,且与抛物线交于 , 两点, 为抛物线上一动点(不与 , 重合).
(1)求抛物线的解析式;
(2)当点 在直线 下方时,过点 作 轴交 于点 , 轴交 于点 ,求 的最大值.
(3)设 为直线 上的点,以 , , , 为顶点的四边形能否构成平行四边形?若能,求出点 的坐标;若不能,请说明理由.

问题背景:已知 的顶点 在 的边 所在直线上(不与 , 重合), 交 所在直线于点 , 交 所在直线于点 ,记 的面积为 , 的面积为 .
(1)初步尝试:如图①,当 是等边三角形, , ,且 , 时,则 ;
(2)类比探究:在(1)的条件下,先将点 沿 平移,使 ,再将 绕点 旋转至如图②所示位置,求 的值;
(3)延伸拓展:当 是等腰三角形时,设 .
(Ⅰ)如图③,当点 在线段 上运动时,设 , ,求 的表达式(结果用 , 和 的三角函数表示).
(Ⅱ)如图④,当点 在 的延长线上运动时,设 , ,直接写出 的表达式,不必写出解答过程.

某太阳能热水器的横截面示意图如图所示,已知真空热水管 与支架 所在直线相交于点 ,且 ,支架 与水平线 垂直, , , .
(1)求支架 的长;
(2)求真空热水管 的长.(结果保留根号)

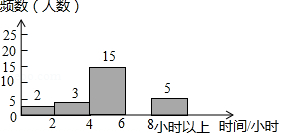
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
|
课外阅读时间(单位:小时) |
频数(人数) |
频率 |
|
|
2 |
0.04 |
|
|
3 |
0.06 |
|
|
15 |
0.30 |
|
|
|
0.50 |
|
|
5 |
|
请根据图表信息回答下列问题:
(1)频数分布表中的 , ;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人?