如图,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的1/4圆周轨道,半径OA处于水平位置,BDO是直径为15m的半圆轨道,D为BDO轨道的中央,一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的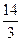 倍,取g=10m/s2.
倍,取g=10m/s2.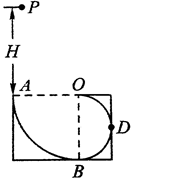
H的大小等于多少?
试讨论此球能否到达BDO轨道的O点,并说明理由。
小球沿轨道运动后再次落到轨道上前瞬间的速度大小是多少?
小车从静止开始以1m/s2的加速度前进,车后相距x0=25m处,与车运动方向相同的某人同时开始以6m/s的速度匀速追车,问能否追上?若追不上,求人、车间的最小距离是多少?
如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到175m时,以10m/s的速度向上匀速运动,同时有一颗质量为0.01kg的小铆钉从热气球上脱离掉落,小铆钉脱离时相对热气球静止。若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2。求:
(1)热气球所受浮力大小;
(2)匀速上升时热气球所受的空气阻力;
(3)小铆钉落地时热气球离地的高度。
为了提高运动员奔跑时下肢向后的蹬踏力量,在训练中,让运动员腰部系绳拖汽车轮胎奔跑,已知运动员在奔跑中拖绳上端与在面的高度为1.2m,且恒定,轻质无弹性的拖绳长2m,运动员质量为60kg,车胎质量为12kg,车胎与跑道间的动摩擦因数为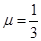 ,如图甲所示,将运动员某次拖胎奔跑100m当做连续过程,抽象处理后的v-t图象如图乙所示,g=10m/s2,不计空气阻力。求:
,如图甲所示,将运动员某次拖胎奔跑100m当做连续过程,抽象处理后的v-t图象如图乙所示,g=10m/s2,不计空气阻力。求: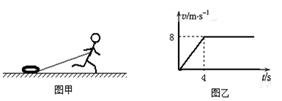
(1)运动员加速过程中的加速度大小a及跑完100m后用的时间t;
(2)在加速阶段绳子对轮胎的拉力大小T及运动员与地面间的摩擦力大小f人。
放风筝是春天时大人、小孩都爱玩的一项有趣的体育活动,手上牵着线拉着风筝迎风向前跑,就可以将风筝放飞到高处,有一个小朋友将一只重为4N的风筝放飞到一定高度后,便拉住线的下端以一定的速度匀速跑动,线恰能与水平面成53°角保持不变,这时小朋友拉住线的力为5N,求风筝所受的风力大小和方向(sin53°= )
)
汽车在路上出现故障时,应在车后放置三角警示牌(如图所示),以提醒后面驾车司机,减速安全通过。在夜间,有一货车因故障停驶,后面有一小轿车以30m/s的速度向前驶来,由于夜间视线不好,小轿车驾驶员只能看清前方50m的物体,并且他的反应时间为0.6s,制动后最大加速度为5m/s2。求:
(1)小轿车从刹车到停止所用的最短时间;
(2)三角警示牌至少要放在车后多远处,才能有效避免两车相撞。