如图所示,在垂直纸面向里的匀强磁场的边界上,有两个质量和电量均相同的正、负离子(不计重力),从点O以相同的速度先后射入磁场中,入射方向与边界成q角,则正、负离子在磁场中 ( )
| A.运动时间相同 | B.运动轨迹的半径相同 |
| C.重新回到边界时速度的大小和方向相同 | D.重新回到边界的位置与O点距离不相等 |
一质点沿直线Ox方向做加速运动,它离开O点的距离随时间变化的关系为
s=4+2t3(m),它的速度随时间变化的关系为v=6t2(m/s).则该质点在t=2 s时的瞬时速度和t=0到t=2 s间的平均速度分别为( )
| A.8 m/s、24 m/s |
| B.24 m/s、8 m/s |
| C.24m/s、10 m/s |
| D.24 m/s、12 m/s |
如图所示,MNP为竖直面内一固定轨道,其1/4圆弧段MN与水平段NP相切于NP端固定一竖直挡板,NP长度为2m,圆弧半径为1m。一个可视为质点的物块自.M端 从静止开始沿轨道下滑,与挡板发生碰撞(只改变速度方向而不改变速度大小)后,最 终停止在水平轨道上某处。已知物块在MN段的摩擦可忽略不计,与NP段轨道间的滑动摩擦因数为0.2。则物块()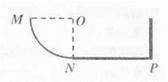
| A.运动过程中与挡板发生2次碰撞 |
| B.返回圆弧轨道的最大髙度为0.6m |
| C.在NP间往返一次克服摩擦力作功8J |
| D.第一与第二次经过圆轨道上N点时对轨道的压力之比为15:7 |
利用传感器和计算机可以测量快速变化的力的瞬时值。实验时,把小球举高到弹性绳子的悬点O 处,然后放手让小球自由下落。图是用这种方法获得的弹性绳中拉力随时间的变化图线。由图所提供的信息,以下正确的是( ) 
| A.t2时刻小球速度最大 |
| B.小球和弹性绳组成的系统机械能不守恒 |
| C.t1到t2期间小球速度一直减小到零 |
| D.t1到t2期间小球重力势能减少量小于弹性绳弹性势能增加量 |
在倾角为30°高为h的斜面顶端,将一个小球沿水平方向抛出,抛出时小球的速度 ,设小球在空中飞行到达某一位置的位移与水平方向的夹角
,设小球在空中飞行到达某一位置的位移与水平方向的夹角 ,速度与水平方向的夹角为
,速度与水平方向的夹角为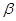 ,则()
,则()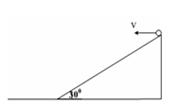
A.一定是 |
B. 可能大于 可能大于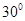 |
C.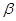 可能大于 可能大于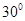 |
D.若使初速度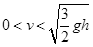 ,小球都将落到斜面上,且其速度方向与斜面的夹角将相同 ,小球都将落到斜面上,且其速度方向与斜面的夹角将相同 |
如图所示,重球m用一条不可伸长的轻质细线栓住后悬于O点,重球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置(a)匀速向左移动到位置(b),在此过程中,正确说法是()
| A.球与劈之间的摩擦力对球做正功; |
| B.劈与球之间的摩擦力对球做负功; |
| C.F对劈所做的功与球对劈所做的功的绝对值相等。 |
| D.劈对球的弹力对球所做的功与球对劈的弹力对劈所做的功的绝对值不相等 |