如图所示,某行星围绕太阳C沿椭圆轨道运行.它的近日点A离太阳的距离为a,行星经过近日点时的速率为va,行星的远日点B离太阳的距离为b,求它经过远日点时速度的大小是 ( )
 B.
B.  C.
C.  D.
D. 
如图所示,小球用细绳系住,绳的另一端固定与O点,现用水平力F缓慢的推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力 以及绳对小球的拉力
以及绳对小球的拉力 的变化情况是
的变化情况是
A. 保持不变, 保持不变, 不断增大 不断增大 |
B. 不断增大, 不断增大, 不断减小 不断减小 |
C. 保持不变, 保持不变, 先增大后减小 先增大后减小 |
D. 不断增大, 不断增大, 先减小后增大 先减小后增大 |
L形木板P(上表面光滑)放在固定斜面上,轻质弹簧一端固定在木板上,另一端与置于木板上表面的滑块Q相连,如图所示,若P、Q一起沿斜面匀速下滑,不计空气阻力,则木板P的受力个数为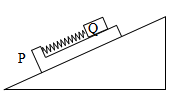
| A.3 | B.4 | C.5 | D.6 |
如图所示,一个人站在水平地面上的长木板上用力F向右推箱子,木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g,则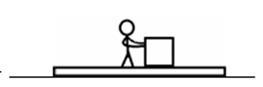
| A.箱子受到的摩擦力方向向右 |
| B.地面对木板的摩擦力方向向左 |
| C.木板对地面的压力大小为3mg |
| D.若人用斜向下的力推箱子,则木板对地面的压力会大于3mg |
如图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用静止与P点,设滑块所受支持力为 ,OP与水平方向的夹角为
,OP与水平方向的夹角为 ,下列关系正确的是
,下列关系正确的是
A. |
B. |
C. |
D. |
下列四组共点力分别作用在同一物体上,有可能使物体做匀速直线运动的是
| A.3N、9N、5N | B.4N、2N、7N | C.4N、14N、5N | D.3N、4N、5N |