设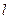 ,
,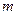 是两条不同的直线,
是两条不同的直线,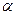 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若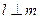 , ,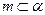 ,则 ,则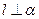 |
B.若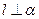 , ,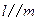 ,则 ,则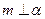 |
C.若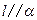 , ,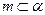 ,则 ,则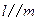 |
D.若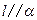 , ,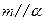 ,则 ,则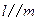 |
曲线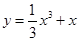 在点(1,
在点(1,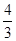 )处的切线与坐标轴围成的三角面积为()
)处的切线与坐标轴围成的三角面积为()
A.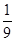 |
B. |
C.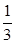 |
D. |
用数学归纳法证明不等式: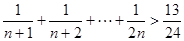 (
(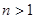 ,
,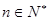 ),在证明
),在证明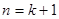 这一步时,需要证明的不等式是()
这一步时,需要证明的不等式是()
A.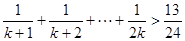 |
B.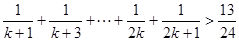 |
C.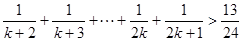 |
D.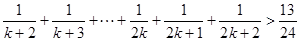 |
设随机变量 服从正态分布
服从正态分布 ,则
,则 ( )
( )
A. |
B. |
C.1-2 |
D.1- |
(1)已知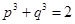 ,求证:
,求证: .用反证法证明时,可假设
.用反证法证明时,可假设 ;
;
(2)若 ,
, ,求证:方程
,求证:方程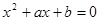 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根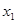 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设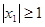 ;
;
以下结论正确的是( )
| A.(1)与(2)的假设都错误 | B.(1)的假设正确;(2)的假设错误 |
| C.(1)与(2)的假设都正确 | D.(1)的假设错误;(2)的假设正确 |
若复数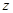 满足
满足 (
( 是虚数单位),则
是虚数单位),则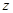 的共轭复数为()
的共轭复数为()
A. |
B.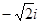 |
C.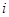 |
D. |