（本题6分）
如图，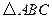
内接于⊙O，点
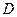在半径
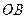的延长线上，
．
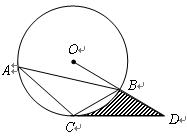
（1）试判断直线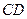
与⊙O的位置关系，并说明理由；
（2）若⊙O的半径长为1，求由弧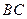
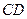、线段和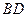
所围成的阴影部分面积（结果保留
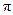和根号）．
已知二次函数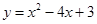
.
（1）求顶点坐标和对称轴方程；
（2）求该函数图象与x标轴的交点坐标；
（3）指出x为何值时，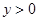
；当x为何值时，
.
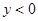如图，已知在⊙O中，弦AB的长为8cm，半径为5 ㎝， 过O作OC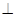
AB求点O与AB的距离．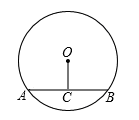
如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE=0.4m，EF=0.2cm，测得边DF离地面的高度AC=1.5m，CD=8m，求树高.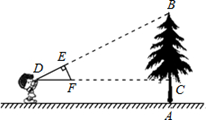
已知：如图，Rt△ABC中，CD是斜边AB上的高.求证:AC2=AD·AB
阅读探索：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
（1）当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：
设所求矩形的两边分别是x和ｙ，由题意得方程组：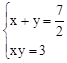
，
消去y化简得：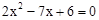
，
∵△＝49－48>0，∴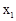
=，
=.
∴满足要求的矩形B存在.
（2）如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B.
（3）如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？