已知数列 和
和 中,数列
中,数列 的前
的前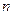 项和记为
项和记为 . 若点
. 若点 在函数
在函数
的图象上,点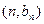 在函数
在函数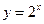 的图象上
的图象上
(Ⅰ)求数列 的通项公式
的通项公式
(Ⅱ)求数列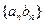 的前
的前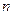 项和
项和
已知 ,若
,若 ,
,
 ,
,
(1)求 ;
;
(2)求 的夹角。
的夹角。
(本小题满分 12分)
12分)
根据下面的要求,求满足 的最小的自然数n。
的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)下图是解决该问题的一个程序,但有2处错误,请找出错误并予以更正。
(本小题满分10分)
若 ,
, ,且
,且 ,
, ,求下列各值.
,求下列各值.
(1)  (2)
(2) 
已知函数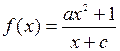
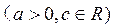 为奇函数,当
为奇函数,当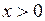 时,
时, 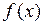 的最小值为2.
的最小值为2.
(I)求函数的解析式
(Ⅱ)若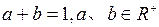 ,求证:
,求证: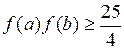
(Ⅲ) 若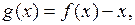
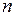
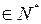 且
且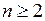 ,求证:
,求证: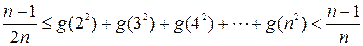
为了竖一块广告牌,要制造三角形支架 ,三角形支架如图所示 . 要求∠ACB=60°,BC长度大于 1 米,且AC比AB长 0.5 米 . 为了广告牌稳固,要求AC 的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?