如图所示，物体A放在足够长的木板B上，木板B静止于水平面。t = 0时，电动机通过水平细绳以恒力F拉木板B，使它做初速度为零，加速度aB = 1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mg均为2.0kg，A、B之间的动摩擦因数μ1 = 0.05，B与水平面之间的动摩擦因数μ2 = 0.1，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度g取10m/s2。求
物体A刚运动时的加速度aA
t = 1.0s时，电动机的输出功率P；
若t = 1.0s时，将电动机的输出功率立即调整为P′ = 5W，并在以后的运动过程中始终保持这一功率不变，t = 3.8s时物体A的速度为1.2m/s。则在t = 1.0s到t = 3.8s这段时间内木板B的位移为多少？
如图所示，小球沿光滑的水平面冲上一个光滑的半圆形轨道，已知轨道的半径为R，小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力。请求出：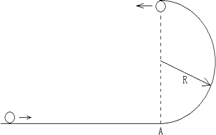
（1）小球到达轨道最高点时的速度为多大？
（2）小球落地时距离A点多远？落地时速度多大？
如图所示，光滑水平地面上有一足够长的木板，左端放置可视为质点的物体，其质量为m1=1kg,木板与物体间动摩擦因数u=0.1。二者以相同的初速度Vo="0.8m/s" —起向右运动，木板与竖直墙碰撞时间极短，且没有机械能损失。重力加速度g =10 m /s2。
I .如果木板质量m2=3kg,求物体相对木板滑动的最大距离；
II.如果木板质量m2=0.6kg,求物体相对木板滑动的最大距离。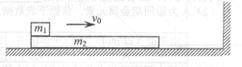
一束单色光斜着射向并穿过一厚度为d的玻璃砖。已知该玻璃砖对单色光的折射率为n,单色光的入射角为a,光在真空中的传播速度为C。
求：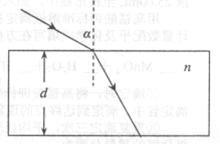
I .若入射角a=60°,且已知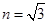
。求该色光经玻璃砖折射后的折射角；
II.该色光穿过玻璃砖所用的时间与入射角a和折射率n的关系。
如图所示，一长为L、内横截面积为S的绝热气缸固定在水平地面上，气缸内用一质量为m的绝热活塞封闭了一定质量的理想气体，幵始时活塞用销钉固定在气缸正中央，气缸内被封闭气体压强为P,外界大气压为Po (P>P0)，现释放活塞，测得活塞被缸内气体推到缸口时的速度为V。求：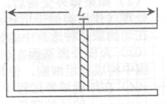
I .此过程克服大气压力所做的功；
II.活塞从释放到将要离开缸口，缸内气体内能改变了多少？
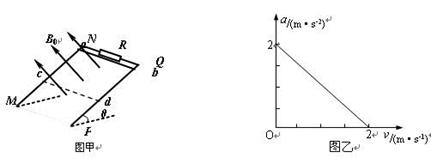
如图甲所示，MN、PQ为间距L=0.5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角θ=37°，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。（取g=10m/s2，sin37°=0.6，cos37°=0.8）。求：
（1）金属棒与导轨间的动摩擦因数μ（2）cd离NQ的距离s
（3）金属棒滑行至cd处的过程中，电阻R上产生的热量
（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化（写出B与t的关系式）。