同学们,我们在本期教材的第一章《有理数》中曾经学习过绝对值的概念:一般的,数轴上表示数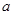 的点与原点的距离叫做数
的点与原点的距离叫做数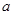 的绝对值,记作
的绝对值,记作 。
。
实际上,数轴上表示数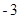 的点与原点的距离科技做
的点与原点的距离科技做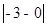 :数轴上表示数
:数轴上表示数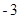 的点与表示数
的点与表示数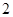 的点的距离可记作
的点的距离可记作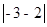 ,那么,
,那么,(I) ①数轴上表示数
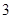 的点与表示数1的点的距离可记作________
的点与表示数1的点的距离可记作________
②数轴上表示数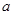 的点与表示数2的点的距离可记作________
的点与表示数2的点的距离可记作________
③数轴上表示数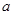 的点与表示数-3的点的距离可记作________
的点与表示数-3的点的距离可记作________(II)数轴上表示到数-2的点的距离为5的点有几个?并求出它们表示的数。
(III)根据(I)中②、③两小题你所填写的结论,请同学们利用数轴探究这两段距离之和的最小值,并简述你的思考过程。
(眉山)(本小题满分11分)如图,已知抛物线 的顶点D的坐标为(1,
的顶点D的坐标为(1, ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
(泸州)如图,一次函数 (
( )的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
(1)求该一次函数的解析式;
(2)若反比例函数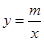 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.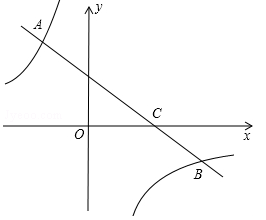
(泸州)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
(泸州)如图,已知二次函数的图象M经过A(﹣1,0),B(4,0),C(2,﹣6)三点.
(1)求该二次函数的解析式;
(2)点G是线段AC上的动点(点G与线段AC的端点不重合),若△ABG与△ABC相似,求点G的坐标;
(3)设图象M的对称轴为l,点D(m,n)( )是图象M上一动点,当△ACD的面积为
)是图象M上一动点,当△ACD的面积为 时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
(凉山州)如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.