某一中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问: 聪聪家与刚刚家相距多远?
如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
聪聪家向西210米所表示的数是多少?
你认为可用什么办法求数轴上两点之间的距离?
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE∶S△DCB=1∶3,求S△DCE∶S△ABD.
在比例尺为1∶50000的地图上,一块多边形地区的周长是72 cm,多边形的两个顶点A、B之间的距离是25 cm,求这个地区的实际边界长和A、B两地之间的实际距离.
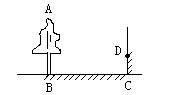
如图,阳光透过窗口照到室内,在地面上留下2.7米宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7米,窗口高AB="1.8" 米,试求窗口下底与地面之间的距离BC的大小。
我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。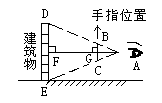
一位同学想利用树影测出树高,他在某时刻测得直立的标杆高1米,影长是0.9米,但他去测树影时,发现树影的上半部分落在墙CD上,(如图所示)他测得BC=2.7米,CD=1.2米。你能帮他求出树高为多少米吗?