(已知,如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=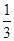 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为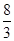 .(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
.(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求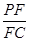 的值.
的值.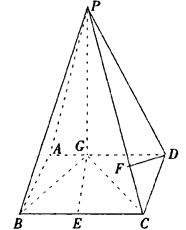
如图,在三棱柱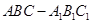 中,
中,
每个侧面均为正方形,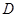 为底边
为底边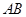 的中点,
的中点,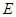 为侧棱
为侧棱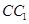 的中点.
的中点.
(Ⅰ)求证: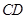 ∥平面
∥平面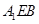 ;
;
(Ⅱ)求证: 平面
平面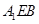 ;
;
(Ⅲ)求直线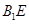 与平面
与平面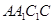 所成角的正弦值.
所成角的正弦值. 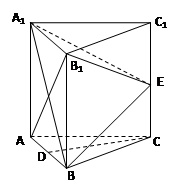
(本小题满分14分)
从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组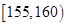 、第二组
、第二组 ;…第八组
;…第八组 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,求满足
,求满足 的事件概率.
的事件概率.
(本小题满分14分)
在三角形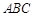 中,
中, 、
、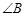 、
、 的对边分别为
的对边分别为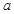 、
、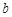 、
、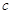 ,若
,若 (Ⅰ)求
(Ⅰ)求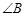 的大小。(Ⅱ)若
的大小。(Ⅱ)若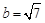 、
、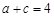 ,求三角形
,求三角形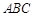 的面积.
的面积.
已知向量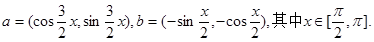
(1)若 求x的值;
求x的值;
(2)函数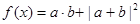 ,若
,若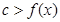 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围.