如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场,磁场方向垂直于纸面向里,磁感应强度B=5/3T;电场方向竖直向上,场强E=mg/q=10N/C,一质量为m=2×10-5kg,电荷量q=+2×10-5C的小球从边界上N点正上方高为h=0.2m处的M点静止释放,下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块,已知爆炸后A向上运动,能达到的最大高度为4h;B向下运动进入电磁场区域,此后A也将进入电磁场区域.g=10m/s2求: B刚进入电磁场区域的速度v1?
B第二次进入电磁场区域的速度v2?

设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.
如图所示,质量分别为2m和m的两物体A、B叠放在一起,放在光滑的水平地面上,已知A、B间的最大摩擦力为A物体重力的μ倍,若用水平力分别作用在A或B上,使A、B保持相对静止做加速运动,则作用于A、B上的最大拉力FA与FB之比为
一物块质量 静止置于光滑水平面上,受到一个如图所示的力F的作用在水平面内运动,力F是一个周期性变化的力,规定向东为力F的正方向,求:
静止置于光滑水平面上,受到一个如图所示的力F的作用在水平面内运动,力F是一个周期性变化的力,规定向东为力F的正方向,求:
(1)第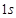 内和第
内和第 内的加速度大小
内的加速度大小
(2) 时物块离开出发点的位移大小
时物块离开出发点的位移大小
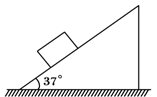
如图所示,在倾角为 的固定斜面上静置一个质量为
的固定斜面上静置一个质量为 的物体,物体与斜面间的动摩擦因数为
的物体,物体与斜面间的动摩擦因数为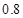 ,求(
,求( ,
, ,
, )
)
(1)物体所受的摩擦力;
(2)若改用沿斜面向上的力拉物体,使之向上匀速运动,则拉力是多少?
如图所示,小球被轻质细绳系住斜吊着放在光滑斜面上,小球与斜面均处于静止状态,设小球质量 ,斜面倾角
,斜面倾角 ,细绳与竖直方向夹角
,细绳与竖直方向夹角 ,光滑斜面体的质量
,光滑斜面体的质量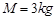 ,置于粗糙水平面上(
,置于粗糙水平面上( )求:
)求:
(1)细绳对小球拉力的大小;
(2)地面对斜面体的摩擦力的大小和方向
从离地 的空中由静止开始自由落下一个小球,忽略空气阻力,取
的空中由静止开始自由落下一个小球,忽略空气阻力,取 ,求:
,求:
(1)经过多少时间落到地面;
(2)小球落地过程中完成最后 的时间;
的时间;