已知实数
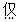 满足
满足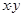 >0,且
>0,且 ,则xy取值的范围是( )
,则xy取值的范围是( )
A.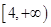 |
B. |
C.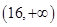 |
D.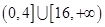 |
设有一正态总体,它的概率密度曲线是函数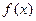 的图象,且
的图象,且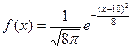 ,则这个正态总体的均值与标准差分别是()
,则这个正态总体的均值与标准差分别是()
| A.10与8 | B.10与2 | C.8与10 | D.2与10 |
正态总体N(0,1)在区间(-2,-1)和(1,2)上取值的概率分别为p1、p2,则
| A.p1>p2 | B.p1<p2 | C.p1=p2 | D.不确定 |
某厂生产的零件外直径X~N(8.0,0.152),单位mm,今从该厂上、下午生产的零件中各随机取出一个,测得其外直径分别为7.9mm和7.5mm,则可认为()
| A.上、下午生产情况均为正常 | B.上、下午生产情况均为异常 |
| C.上午生产情况正常,下午生产情况异常 | D.上午生产情况异常,下午生产情况正常 |
N(0,1)的概率密度函数是()
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.既奇又偶函数 |
把一条正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b,下列说法中不正确的是()
| A.曲线b仍然是正态曲线 | B.曲线a和曲线b的最高点的纵坐标相等 |
| C.以曲线b为正态分布的总体的方差比以曲线a为正态分布的总体的方差大2 | |
| D.以曲线b为正态分布的总体的期望比以曲线a为正态分布的总体的期望大2 |