(12分)(1)随着科技的迅猛发展和人们生活水平的提高，下列问题一定能够实现或完成的是 ( )
| A．假如全世界60亿人同时数1 g水的分子个数，每人每小时可以数5000个，不间断地数，则大约20年能数完(阿伏加德罗常数NA取6.0×1023个/mol) |
| B．热量可以从低温物体传到高温物体 |
| C．热机的效率达到100 % |
| D．太阳能的利用普及到老百姓的日常生活中 |
(2)某学校研究性学习小组组织开展一次探究活动，想估算地球周围大气层空气的分子个数和早晨同中午相比教室内的空气的变化情况．一学生通过网上搜索，查阅得到以下几个物理量数据：地球的半径R＝6.4×106 m，地球表面的重力加速度g＝9.8 m/s2，大气压强p0＝1.0×105 Pa，空气的平均摩尔质量M＝2.9×10－2 kg/mol，阿伏加德罗常数NA＝6.0×1023个/mol.另一个同学用温度计测出早晨教室内的温度是7℃，中午教室内的温度是27℃.
①第一位同学根据上述几个物理量能估算出地球周围大气层空气的分子数吗？若能，请说明现由；若不能，也请说明理由．
②根据上述几个物理量能否估算出中午跑到教室外的空气是早晨教室内的空气的几分之几？
如图所示，坡道顶端距水平面高度为h，质量为m1的小物块A从坡道顶端由静止滑下，进入水平面上的滑道时无机械能损失，为使A制动，将轻弹簧的一端固定在水平滑道延长线M处的墙上，另一端与质量为m2的挡板B相连，弹簧处于原长时，B恰位于滑道的末端O点。A与B碰撞时间极短，碰后结合在一起共同压缩弹簧，已知在OM段A、B与水平面间的动摩擦因数均为μ，其余各处的摩擦不计，重力加速度为g，求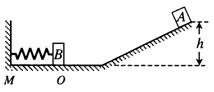
(1)物块A在与挡板B碰撞前瞬间速度v的大小；
(2)弹簧最大压缩量为d时的弹性势能EP(设弹簧处于原长时弹性势能为零)。
光滑水平面上放着质量mA="1" kg的物块A与质量mB="2" kg的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B不动，此时弹簧弹性势能Ep="49" J。在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，如图所示。放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R="0.5" m，B恰能到达最高点C。取g="10" m/s2，求：
（1）绳拉断后瞬间B的速度vB的大小；
（2）绳拉断过程绳对B的冲量I的大小；
（3）绳拉断过程绳对A所做的功W。
有两个完全相同的小滑块A和B，A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰，碰撞中无机械能损失。碰后B运动的轨迹为OD曲线，如图所示。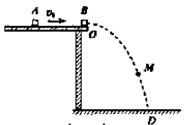
（1）已知滑块质量为m，碰撞时间为
，求碰撞过程中A对B平均冲力的大小。
（2）为了研究物体从光滑抛物线轨道顶端无初速下滑的运动，特制做一个与B平抛轨迹完全相同的光滑轨道，并将该轨道固定在与OD曲线重合的位置，让A沿该轨道无初速下滑（经分析，A下滑过程中不会脱离轨道）。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系；
b.在OD曲线上有一M点，O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
一倾角为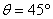
的斜面固定于地面，斜面顶端离地面的高度h0=1m，斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块（视为质点）。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后，将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中，挡板给予小物块的总冲量是多少？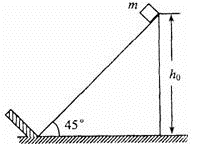
图中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点O由一不可伸长的轻绳相连，轻绳长为l。开始时，轻绳处于水平拉直状态，小球和滑块均静止。现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有粘住物质的固定挡板粘住，在极短的时间内速度减为零。小球继续向左摆动，当轻绳与竖直方向的夹角θ＝60°时小球达到最高点。求
（1）从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量；
（2）小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小。