定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系 中,若
中,若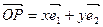 (其中
(其中 、
、 分别是斜坐标系
分别是斜坐标系 轴、
轴、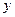 轴正方向上的单位向量,
轴正方向上的单位向量, ,
, 为坐标原点),则有序实数对
为坐标原点),则有序实数对 称为点
称为点 的斜坐标. 如图所示,在平面斜坐标系
的斜坐标. 如图所示,在平面斜坐标系 中,若
中,若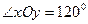 ,点
,点 ,
, 为单位圆上一点,且
为单位圆上一点,且 ,点
,点 在平面斜坐标系中的坐标是
在平面斜坐标系中的坐标是
A. |
B. |
C. |
D. |
已知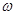 >0,函数f(x)=sin(
>0,函数f(x)=sin(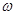 x+
x+ )在(
)在(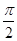 ,
,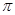 )上单调递减,则
)上单调递减,则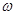 的取值范围是()
的取值范围是()
A.[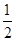 , ,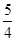 ] ] |
B.[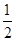 , , ] ] |
C.[0,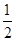 ] ] |
D. |
设函数f(x)=sin( x+
x+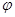 )+cos(
)+cos( x+
x+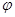 )(
)( >0,|
>0,|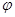 |<
|<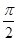 )的最小正周期为π,且f(-x)=f(x),则( )
)的最小正周期为π,且f(-x)=f(x),则( )
A.y=f(x)在(0,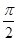 )单调递减 )单调递减 |
B.y=f(x)在(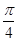 , ,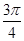 )单调递减 )单调递减 |
C.y=f(x)在(0,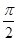 )单调递增 )单调递增 |
D.y=f(x)在(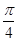 , ,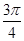 )单调递增 )单调递增 |
已知函数f(x)=sin(2x+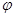 ),其中
),其中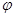 为实数,若f(x)≤|f(
为实数,若f(x)≤|f( )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f(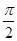 )>f(
)>f(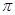 ),则f(x)的单调递增区间是()
),则f(x)的单调递增区间是()
A.[ - -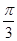 , , + + ](k∈Z) ](k∈Z) |
B.[ , , + +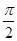 ](k∈Z) ](k∈Z) |
C.[ + + , , + +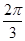 ](k∈Z) ](k∈Z) |
D.[ - -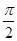 , , ](k∈Z) ](k∈Z) |
函数y=sin(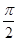 +x)cos(
+x)cos( -x)的最大值为()
-x)的最大值为()
A.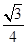 |
B. |
C.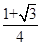 |
D.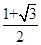 |
设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ= ( )
A.- |
B. |
C.- |
D. |