如图所示,一小型发电机内有n=100匝矩形线圈,线圈面积S=0.10m2,线圈电阻为1Ω。在外力作用下矩形线圈在B=0.10T匀强磁场中,以恒定的角速度ω="100π" rad/s绕垂直于磁场方向的固定轴OO′匀速转动,发电机线圈两端与R =9Ω的电阻构成闭合回路。求(1)线圈转动时产生感应电动势的最大值(2)从线圈平面通过中性面时开始,线圈转过90º角的过程中通过电阻R横截面的电荷量(3)写出电阻R两端电压瞬时值的表示式(当线圈平面与磁场垂直时开始计时)(4)线圈匀速转动10s,电流通过电阻R产生的焦耳热(π2=10)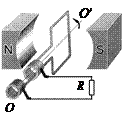
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑的圆孤轨道下滑。B、C为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角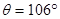 ,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的动摩擦因数为
,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的动摩擦因数为 =
= (g=10m/s2,sin37°=0.6,cos37°=0.8)
(g=10m/s2,sin37°=0.6,cos37°=0.8)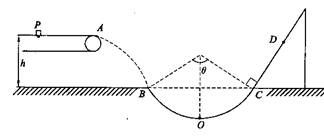
试求:(1)小物块离开A点时的水平初速度v1。(2)小物块经过O点时对轨道的压力。
(3)假设小物块与传送带间的动摩擦因数为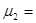 0.3,传送带的速度为5m/s,则PA间的距离是多少?
0.3,传送带的速度为5m/s,则PA间的距离是多少?
(4)斜面上CD间的距离。
如图所示,粗糙弧形轨道和两个光滑半圆轨道组成翘尾巴的S形轨道.光滑半圆轨道半径为R,两个光滑半圆轨道连接处CD之间留有很小空隙,刚好能够使小球通过,CD之间距离可忽略.粗糙弧形轨道最高点A与水平面上B点之间的高度为h.从A点静止释放一个可视为质点的小球,小球沿翘尾巴的S形轨道运动后从E点水平飞出,落到水平地面上,落点到与E点在同一竖直线上B点的距离为s.已知小球质量m,不计空气阻力,求: 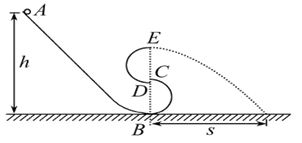
(1)小球从E点水平飞出时的速度大小; (2)小球运动到半圆轨道的B点时对轨道的压力; (3)小球沿翘尾巴S形轨道运动时克服摩擦力做的功.
如图所示,一质量为1 kg的小球套在一根固定的直杆上,直杆与水平面夹角θ为30°。现小球在F="20" N的竖直向上的拉力作用下,从A点静止出发向上运动,已知杆与球间的动摩擦因数μ为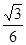 。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。
。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。
从高H处以水平速度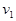 平抛一个小球1,同时从地面以速度
平抛一个小球1,同时从地面以速度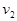 竖直向上抛出一个小球2,两小球在空中相遇则:( )
竖直向上抛出一个小球2,两小球在空中相遇则:( )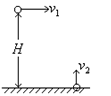
(1).从抛出到相遇所用时间为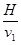 .(2)从抛出到相遇所用时间为
.(2)从抛出到相遇所用时间为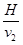
(3).抛出时两球的水平距离是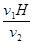 (4).相遇时小球2上升高度
(4).相遇时小球2上升高度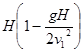
| A.(1)(3) | B.(2)(3) | C.(2)(3)(4) | D.(2)(4) |
如图所示,在真空中的竖直平面内,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B,A球的电荷量为+4q,B球的电荷量为-3q,组成一带电系统.虚线MN与PQ平行且相距3L,开始时PQ恰为杆的中垂线.在MN与PQ间加竖直向上的匀强电场,恰能使带电系统静止不动.现使电场强度突然加倍(已知当地重力加速度为g)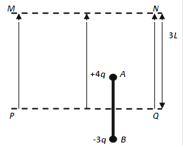
求:
(1)B球刚到达电场边界PQ时的速度大小;
(2)判定A球能否到达电场边界MN,如能,请求出A球到达电场边界MN时的速度大小;如不能,请说明理由。
(3) 带电系统运动过程中,B球电势能增加量的最大值;
(4)带电系统从开始运动到返回原出发点所经历的时间。