如下图所示是游乐场中过山车的实物图片,左图是过山车的模型图。在模型图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接。现使小车(视作质点)从P点以一定的初速度沿斜面向下运动。已知斜轨道面与小车间的动摩擦因数为μ=1/24,g=10m/s2,sin37°=0.6,cos37°=0.8。问:
(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
(2)若小车在P点的初速度为10m/s,则小车能否安全通过两个圆形轨道?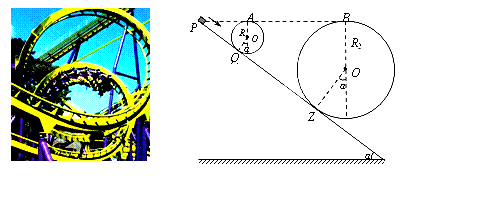
 一辆汽车,以36km/h的速度匀速行驶10s,然后以1m/s2的加速度匀加速行驶10s,求:
一辆汽车,以36km/h的速度匀速行驶10s,然后以1m/s2的加速度匀加速行驶10s,求:
(1)汽车在这20s内的位移是多大?
(2)汽车在加速的10s内的平均速度是多大?
一宇宙人在太空(万有引力可以忽略不计)玩垒球。如图所示,辽阔的太空球场半侧为匀强电场,另半 侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场
侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场 方向与界面垂直,磁场方向垂直纸面向里,电场强度大小
方向与界面垂直,磁场方向垂直纸面向里,电场强度大小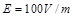 。宇宙人位于电场一侧距界面为
。宇宙人位于电场一侧距界面为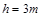 的
的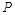 点,
点,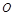 为
为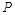 点至界面垂线的垂
点至界面垂线的垂 足,
足, 点位于纸面上
点位于纸面上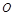 点的右侧,
点的右侧,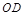 与磁场的方向垂直。垒球的质量
与磁场的方向垂直。垒球的质量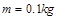 ,电量
,电量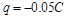 。宇宙人从
。宇宙人从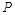 点以初速度
点以初速度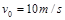 平行于界面投出垒球,要使垒球第一次通过界面时就击中
平行于界面投出垒球,要使垒球第一次通过界面时就击中 点,求:(计算结果保留三位有效数字)
点,求:(计算结果保留三位有效数字)
(1)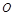 、
、 两点之间的距离。
两点之间的距离。
(2)垒球从抛出到第一次回到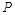 点的时间。
点的时间。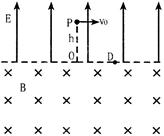
如图所示,光滑导轨与水平面成θ角,导轨宽L。匀强磁场磁感应强度为B。金属杆长也为L,质量为m,水平放在导轨上。当回路总电流为I1时,金属杆正好能静止。求:
(1)B至少多大?这时B的方向如何?
(2)若保持B的大小不变而将B的方向改为竖直向上,
应把回路总电流I2调到多大才能使金属杆保持静止?
在图甲中,电源的电动势E=9.0V,电源内电阻可忽略不计;G为小量程的电 流表,电流表内阻Rg保持不变,R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示。闭合开关S,当R的温度等于20oC时,电流表示数I1=2mA,则当电流表的示数I2=3.6mA时,热敏电阻R的温度为多少?
流表,电流表内阻Rg保持不变,R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示。闭合开关S,当R的温度等于20oC时,电流表示数I1=2mA,则当电流表的示数I2=3.6mA时,热敏电阻R的温度为多少?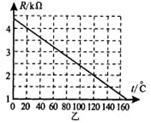

如图所示,在一个倾斜的长冰道上方,一群孩子排成队,每隔1 s有一个小孩往下滑.一游客对着冰道上的孩子拍下一张照片,照片上有甲、乙、丙、丁四个孩子.他根据照片与实物的比例推算出乙与甲和丙两孩 子间的距离分别为12.5 m和17.5 m.请你据此求解下列问题
子间的距离分别为12.5 m和17.5 m.请你据此求解下列问题
(1)小孩下滑的加速度大小a。
(2)拍照时,最下面的小孩丁的速度是多少?
(3)拍照时,在小孩甲上面的冰道上下滑的小孩不会超过几人