为了研究过山车的原理，物理小组提出了下列的设想：取一个与水平方向夹角为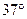
，长为L=2．0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接，如图所示。一个小物块以初速度
，从某一高处水平抛出，到A点时速度方向恰沿AB方向，并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数
（g取l0m／s2，sin37°=0．6，cos37°=0．80）求：
（1）小物块的抛出点和A点的高度差；
（2）为了让小物块不离开轨道，并且能够滑回倾斜轨道AB，则竖直圆轨道的半径应该满足什么条件。
（3）要使小物块不离开轨道，并从水平轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件．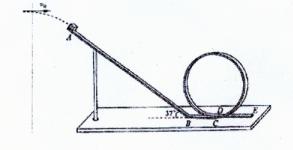
如图所示，在同一竖直平面上，质量为2m的小球A静止在光滑斜面的底部，斜面高度为H=2L，小球受到弹簧的弹性力作用后，沿斜面向上运动。离开斜面后，达到最高点时与静止悬挂在此处的小球B发生碰撞，碰撞中无机械能损失，碰撞后球B刚好能摆到与悬点O同一高度，球A沿水平方向抛射落在水平面C上的P点，O点的投影O＇与P点的距离为L/2。已知球B质量为m，悬绳长L，视两球为质点，重力加速度为g，不计空气阻力，求：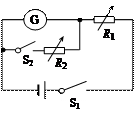
（1）球B在两球碰撞后一瞬间的速度大小；
（2）弹簧的最大弹性势能。
如图所示，相距为L的足够长光滑平行金属导轨水平放置，处于磁感应强度为B，方向竖直向上的匀强磁场中。导轨一端连接一阻值为R的电阻，导轨本身的电阻不计，一质量为m，电阻为r的金属棒ab横跨在导轨上，如图所示。现对金属棒施一恒力F，使其从静止开始运动。求：
（1）运动中金属棒的最大速度为多大？
（2）金属棒的速度为最大速度的四分之一时,
①求ab金属棒的加速度
②求安培力对ab金属棒做功的功率
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。利用双星系统中两颗恒星的运动特征可推算出它们的总质量。已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量。（引力常量为G）
神舟五号载人飞船在绕地球飞行的第5圈进行变轨，由原来的椭圆轨道变为距地面高度h="342" km的圆形轨道。已知地球半径R=6.37×103 k m，地面处的重力加速度g="10" m/s2。试导出飞船在上述圆轨道上运行的周期T的公式（用h、R、g表示），然后计算周期的数值（保留一位有效数字）。
如图所示，一位质量m =60kg参加“挑战极限”的业余选手，要越过一宽度为s=2.5m的水沟，跃上高为h=2.0m的平台，采用的方法是：人手握一根长L=3.25m的轻质弹性杆一端，从A点由静止开始匀加速助跑，至B点时，杆另一端抵在O点的阻挡物上,接着杆发生形变、同时脚蹬地,人被弹起，到达最高点时杆处于竖直，人的重心在杆的顶端，此刻人放开杆水平飞出，最终趴落到平台上，运动过程中空气阻力可忽略不计．
（1）设人到达B点时速度vB=8m/s，人匀加速运动的加速度a=2m/s2，求助跑距离sAB．
（2）人要到达平台，在最高点飞出时刻速度v至少多大？（取g=10m/s2）