如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、
(-1,0)、(1,0)、(-1,-1)。求经过A、B、C三点的抛物线的表达式;
以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。

某市教育行政部门为了解本市中学生对安全知识的了解程度,随机抽取了部分学生进行测试,测试结果分为三个等级.A.非常了解B.了解较多C.了解较少.如图是根据测试结果绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题.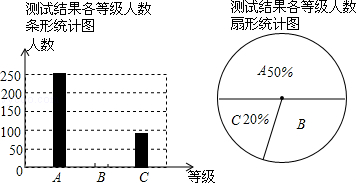
(1)共抽取了多少名学生进行测试?
(2)在条形图中,将表示B的部分补充完整.
(3)在扇形统计图中,计算出C部分所对应的圆心角的度数.
(4)如果全市共24000名中学生,请你估算全市对安全知“了解较少”的中学生人数.
小明上超市买饮料,他看中了盒装牛奶和冰茶,他买了3盒牛奶和4瓶冰茶,共花了29元,已知一盒牛奶和一瓶冰茶价格和为8.5元.一盒牛奶和一瓶冰茶分别需要多少元?
小明和小丽两人玩一个游戏:三张大小,质地都相同相的卡片,分別标有数字1,2,3,将标数字的一面朝下放着,小明从中任意抽取一张,记下数字后放回并洗匀,然后小丽又从中任意抽取一张,记下数字,如果两人抽得的卡片上数字这和为奇数,则小明获胜;如果和为偶数则小丽胜.你认为这个游戏对双方公平吗?谪画树状图或表格分析.
应用无刻度的直尺画图: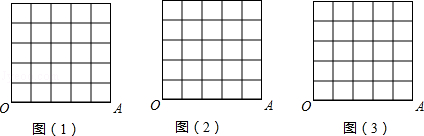
在下面的三个图中,以OA为边,在正方形网格内作∠AOB=α,B点为格点(每个小正方形的顶点)使sinα的值分别为: ,
,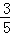 和
和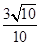 .
.
解不等式组并把解集在数轴上表示出来: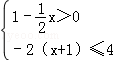 .
.