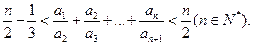(本小题满分16分)
某企业有A、B两种型号的家电产品参加家电下乡活动,若企业投放A、B两种型号家电产品的价值分别为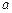 、
、 万元,则农民购买家电产品获得的补贴分别为
万元,则农民购买家电产品获得的补贴分别为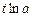 万元、
万元、 万元(
万元( 且为常数).已知该企业投放总价值为100万元的A、B两种型号的家电产品,且A、B两种型号的投放金额都不低于10万元.
且为常数).已知该企业投放总价值为100万元的A、B两种型号的家电产品,且A、B两种型号的投放金额都不低于10万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)问A、B两种型号的家电产品各投放多少万元时,农民得到的总补贴最多?
(本小题满分12分)
在直角坐标 系
系 中,以
中,以 为极点,
为极点,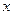 正半轴为极轴建立极坐标系,曲线
正半轴为极轴建立极坐标系,曲线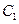 的极坐标方程为
的极坐标方程为 ,
, 分别为
分别为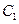 与
与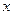 轴,
轴, 轴的交点。曲线
轴的交点。曲线 的参数方程为
的参数方程为 (
( 为参数)。
为参数)。
(1)求 的极坐标,并写出
的极坐标,并写出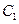 的直角坐标
的直角坐标 方程;
方程;
(2)求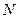 点与曲线
点与曲线 上的动点距离的最大值。
上的动点距离的最大值。
(本小题满分12分)
投到“时尚生活”杂志的稿件,先由两位初审专家进行评审,若能通过两位初审专家的评审,则予以录用;若两位初审专家都未通过,则不予录用;若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则,不予录用.设稿件能通过各初审专家评审的概率均为0.5, 复审的稿件能通过评审的概率为0.3,各位专家独立评审.
复审的稿件能通过评审的概率为0.3,各位专家独立评审.
(1)求投到该杂志的1篇稿件被录用的概率.
(2)若某人投到该杂志3篇稿件,求他被录用稿件篇数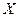 的分布列及期望值.
的分布列及期望值.
(本小题满分12分)
老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格。某同学只能背诵其中的6篇,
试求:(1)抽到他能背诵的课文的数量的分布列;
(2)他能及格的概率。
.(本小题满分10分)
在二项式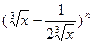 的展开式中,末三项的二项式系数的和等于 37.
的展开式中,末三项的二项式系数的和等于 37.
(1)求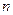 的值;
的值;
(2)求展开式中的第4项;
(
已知数列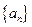 满足
满足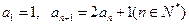 。
。
⑴求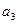 ;
;
⑵求数列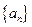 的通项公式;
的通项公式;
⑶证明: