( 10分)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=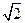 。
。
1)求证:AO 平面BCD;
平面BCD;
2)求异面直线AB与CD所成角的余弦值;
3)求点E到平面ACD的距离。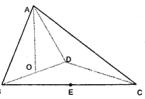
已知函数
(Ⅰ)若 ,求方程
,求方程 的解
的解
(Ⅱ)若关于x的方程 在(0,2)上有两个解
在(0,2)上有两个解 ,求k的取值范围。
,求k的取值范围。
已知集合M是满足下列性质的函数 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意 ,等式
,等式 恒成立。
恒成立。
(Ⅰ)判断一次函数 是否属于集合M;
是否属于集合M;
(Ⅱ)证明 属于集合M,并找到一个常数k;
属于集合M,并找到一个常数k;
(Ⅲ)已知函数 与
与 的图像有公共点,试证明
的图像有公共点,试证明
已知数列 的前n项和为Sn,点
的前n项和为Sn,点 的直线
的直线 上,数列
上,数列 满足
满足 ,
, ,且
,且 的前9项和为153.
的前9项和为153.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,记数列
,记数列 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式 对
对
一切 都成立的最大正整数k的值.
都成立的最大正整数k的值.
设 其导函数
其导函数 的图象经过点
的图象经过点 ,(2,0),如右图所示。
,(2,0),如右图所示。
(Ⅰ)求函数 的解析式和极值;
的解析式和极值;
|
(Ⅱ)对 都有
都有 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
已知函数 是
是 的导函数。
的导函数。
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)若 的值。
的值。