在“验证机械能守恒定律”的实验中，已知打点计时器所用的交流电的频率为50Hz，查得当地的重力加速度g＝9.80m/s2，测得所用的重物的质量为1.00kg，实验中得到一条点迹清晰的纸带如图所示。把第一个点记做O，另选连续的四个点A、B、C、D作为测量的点。经测量知道A、B、C、D四个点到O点的距离分别为62.99cm、70.14cm、77. 67cm、85.58cm。
（1）根据以上数据可知重物由O点运动到C点，重力势能的减少量等于__ _____J；动能的增加量为_____ ___J (取三位有效数字)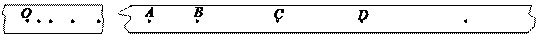
（2）根据以上数据可以计算出重物下落的加速度为___________m/s2(取三位有效数字)，明显小于所查得当地的重力加速度，其主要原因是______________ __________________。
如图表示一架做匀变速直线飞行的飞机的速度一时间图象，利用速度一时间图象可以看出飞机的初速度是_______m/s，10秒后飞机的速度是________ m/s，飞机的速度达到250 m/s， 需要_________秒．
在“探究小车速度随时间变化的规律”的实验中，打点计时器使用的交流电的频率为50 Hz，记录小车运动的纸带如图所示，在纸带上选择0、1、2、3、4、5的6个计数点，相邻两计数点之间还有四个点未画出，纸带旁并排放着带有最小分度为毫米的刻度尺，零点跟“0”计数点对齐，由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中。
| 距离 |
d1 |
d2 |
d3 |
| 测量值／cm |
计算小车通过计数点“2”的瞬时速度为v2 ="______" m/s，小车的加速度是a ="______" m/s2。
某同学在“探究弹力和弹簧伸长的关系”实验中，利用得到的弹力F和弹簧总长度L的数据，作出了F－L图象，如图所示，由此可知：
（1）弹簧不发生形变时的长度L0＝________cm；
（2）弹簧的劲度系数k＝________N/m。
在一次利用滴水法测重力加速度的实验中：让水龙头的水一滴一滴地滴在其正下方的盘子里，调整水龙头让前一滴水滴到盘子而听到声音时，后一滴恰好离开水龙头．从第1次听到水击盘声时开始数“1”并开始计时，数到“n”时停止计时，听到水击盘声的总时间为T，则 每一滴水从水龙头落到盘子处的时间为 ，要得到当地的重力加速度，还需要直接测量的物理量是 ，则当地重力加速度的表达式为。
如图所示，一个质量为m的钢球，放在倾角为θ的固定斜面上，用一竖直挡板挡住，处于静止状态．各个接触面均光滑，重力加速度为g。球对竖直挡板压力的大小是___________，球对斜面的压力的大小是___________；当挡板由竖直位置逆时针缓慢旋转了角α时，球对挡板压力的大小是__________，球对斜面的压力的大小是__________。