有一个带正电的小球,质量为m、电量为q,静止在固定的绝缘支架上.现设法给小球一个瞬时的初速度υ0使小求水平飞出,飞出时小球的电量没有改变.同一竖直面内,有一个竖直固定放置的圆环(圆环平面保持水平),环的直径略大于小球直径,如图所示.要使小球能准确进入圆环,可在空间分布匀强电场或匀强磁场(匀强电场和匀强磁场可单独存在,也可同时存在),请设计两种分布方式,并求出:
(1)相应的电场强度E或磁感应强度B的大小和方向;
(2)相应的小球到圆环的时间t .
(若加匀强电场,则匀强电场限制在竖直面内;若加匀强磁场,则匀强磁场限制在垂直纸面情况.已知υ0> ,小球受重力不能忽略)
,小球受重力不能忽略)
如图所示电路中,电源电动势E=10 V,内阻不计,电阻R1=14 Ω,R2=6.0 Ω, R3=2.0 Ω,R4=8.0 Ω,R5=10 Ω,电容器的电容C=2 μF。求:
(1)电容器所带的电荷量,并说明电容器哪个极板带正电;
(2)若R2突然断路,将有多少电荷量通过R5?流过R5电流的方向如何?
(14分)2012年南昌开始地铁一号线建设,即将于2015年底正式开通运营。假设地铁列车从秋水广场站启动开始匀加速直线运动,然后匀速直线运动,接下来匀减速直线运动到中山西路站停止,已知列车每次加速与减速阶段的加速度大小均相同。设列车加速过程中最大速度为v,显然,v不同,运行时间就不同。下图为技术人员绘制的两站之间的通行时间t与列车最大速度v的关系图像。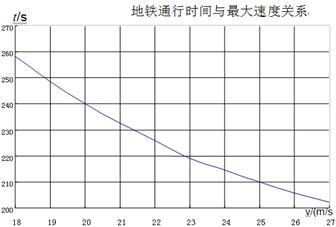
(1)请从图中直接读出从秋水广场站到中山西路站运行时间为t1=240s的情况下列车运行的最大速度v1以及列车最大速度为v2=25m/s时两站间的运行时间t2。
(2)求出秋水广场到中山西路两站之间距离x及列车启动加速度a的大小。
A、B两列火车在同一轨道上同向行驶,A车在前,速度为vA=10m/s,B车在后速度为vB=30m/s.因大雾能见度低,B车在距A车500m时,才发现前方有A车.这时B车立即刹车,已知B车刹车的加速度大小恒为0.25 m/s2.问:
(1)A车若仍按原速前进,两车是否会相撞(通过计算写明你判断的依据)?
(2)B车在刹车的同时发出信号,使A车接收到信号立即加速前进(不考虑接收时间差),则A车的加速度至少是多大时,才能避免事故发生?
重量为100N的木箱放在水平地面上,至少要35N的水平推力,才能使它从原地
开始运动,木箱从原地移动以后,用30N的水平推力就可以使木箱匀速滑动,求:
(1)木箱与地面间的最大静摩擦力。
(2)木箱与地面的动摩擦因数。
南昌八一大桥是江西省第一座斜拉索桥,全长3000多米,设计为双独塔双索面扇形预应力斜拉桥,如图所示。挺拔高耸的103米主塔似一把利剑直刺苍穹,塔两侧的多对钢索连接主梁,呈扇面展开,如巨型琴弦,正弹奏着巨龙腾飞的奏鸣曲.假设斜拉桥中某对钢索与竖直方向的夹角都是53°,每根钢索中的拉力都是5×104N,那么它们对塔柱形成的合力有多大?方向如何?
(已知sin53°=0.8,cos53°=0.6)